概率论中常见分布总结以及python的scipy库使用：两点分布、二项分布、几何分布、泊松分布、均匀分布、指数分布、正态分布

概率分布有两种类型：离散（discrete）概率分布和连续（continuous）概率分布。

离散概率分布也称为概率质量函数（probability mass function）。离散概率分布的例子有伯努利分布（Bernoulli distribution）、二项分布（binomial distribution）、泊松分布（Poisson distribution）和几何分布（geometric distribution）等。

连续概率分布也称为概率密度函数（probability density function），它们是具有连续取值（例如一条实线上的值）的函数。正态分布（normal distribution）、指数分布（exponential distribution）和β分布（beta distribution）等都属于连续概率分布。

1、两点分布（伯努利分布）

伯努利试验：

伯努利试验是在同样的条件下重复地、各次之间相互独立地进行的一种试验。

即只先进行一次伯努利试验，该事件发生的概率为p，不发生的概率为1-p。这是一个最简单的分布，任何一个只有两种结果的随机现象都服从0-1分布。

最常见的例子为抛硬币

其中，

期望E = p

方差D = p*(1-p)^2+(1-p)*(0-p)^2 = p*(1-p)

 2、二项分布（n重伯努利分布）（X~B(n,p））

即做n个两点分布的实验

其中，

E = np

D = np(1-p)

对于二项分布，可以参考https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.binom.html

二项分布的应用场景主要是，对于已知次数n，关心发生k次成功。

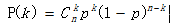，即为二项分布公式可求。

对于抛硬币的问题，做100次实验，观察其概率分布函数：

from scipy.stats import binom
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np

## 设置属性防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

　　首先导入库函数以及设置对中文的支持

fig,ax = plt.subplots(1,1)
n = 100
p = 0.5
#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = binom.stats(n,p,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时，ppf就是p(X<x)=0.01时的x值。
x = np.arange(binom.ppf(0.01, n, p),binom.ppf(0.99, n, p))
ax.plot(x, binom.pmf(x, n, p),'o')
plt.title(u'二项分布概率质量函数')
plt.show()

　　

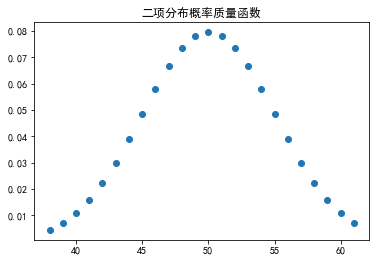
观察概率分布图，可以看到，对于n = 100次实验中，有50次成功的概率（正面向上）的概率最大。

3、几何分布（X ～ GE(p)）

在n次伯努利实验中，第k次实验才得到第一次成功的概率分布。其中：P(k) = (1-p)^(k-1)*p

E = 1/p  推到方法就是利用利用错位相减法然后求lim - k ->无穷 

D = (1-p)/p^2  推到方法利用了D(x) = E(x)^2-E(x^2)，其中E(x^2)求解同上

几何分布可以参考：https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.geom.html#scipy.stats.geom

fig,ax = plt.subplots(1,1)
p = 0.5
#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = geom.stats(p,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时，ppf就是p(X<x)=0.01时的x值。
x = np.arange(geom.ppf(0.01, p),geom.ppf(0.99, p))
ax.plot(x, geom.pmf(x, p),'o')
plt.title(u'几何分布概率质量函数')
plt.show()

　　

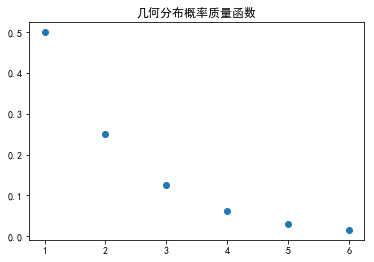
因此，可以看到，对于抛硬币问题，抛个两三次就能成功。

4、泊松分布（X~P(λ)）

描述单位时间/面积内，随机事件发生的次数。P(x = k) = λ^k/k!*e^(-λ)   k = 0,1,2, ...    λ >0

泊松分布可作为二项分布的极限而得到。一般的说，若  ，其中n很大，p很小，因而  不太大时，X的分布接近于泊松分布  。

λ：单位时间/面积下，随机事件的平均发生率

E = λ

D = λ

譬如：某一服务设施一定时间内到达的人数、一个月内机器损坏的次数等。

 假设某地区，一年中发生枪击案的平均次数为2。

fig,ax = plt.subplots(1,1)
mu = 2
#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = poisson.stats(mu,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时，ppf就是p(X<x)=0.01时的x值。
x = np.arange(poisson.ppf(0.01, mu),poisson.ppf(0.99, mu))
ax.plot(x, poisson.pmf(x, mu),'o')
plt.title(u'poisson分布概率质量函数')
plt.show()

　　

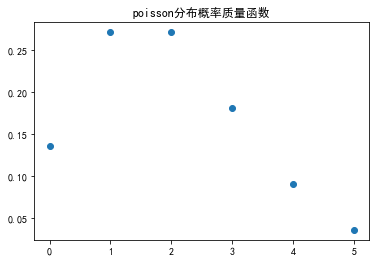
因此，一年内的枪击案发生次数的分布如上所示。

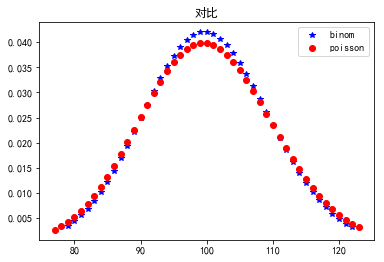
与二项分布对比：

fig,ax = plt.subplots(1,1)

n = 1000
p = 0.1
#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = binom.stats(n,p,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时，ppf就是p(X<x)=0.01时的x值。
x = np.arange(binom.ppf(0.01, n, p),binom.ppf(0.99, n, p))
p1, = ax.plot(x, binom.pmf(x, n, p),'b*',label = 'binom')

mu = n*p
#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = poisson.stats(mu,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时，ppf就是p(X<x)=0.01时的x值。
x = np.arange(poisson.ppf(0.01, mu),poisson.ppf(0.99, mu))
p2, = ax.plot(x, poisson.pmf(x, mu),'ro',label = 'poisson')

plt.legend(handles = [p1, p2])
plt.title(u'对比')
plt.show()

　　

 5、均匀分布（X~U(a,b)）

对于随机变量x的概率密度函数：

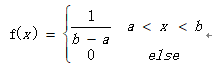
则称随机变量X服从区间[a,b]上的均匀分布。

E = 0.5（a+b）

D = （b-a）^2 / 12

均匀分布在自然情况下极为罕见，而人工栽培的有一定株行距的植物群落即是均匀分布。这表明X落在[a,b]的子区间内的概率只与子区间长度有关，而与子区间位置无关，因此X落在[a,b]的长度相等的子区间内的可能性是相等的，所谓的均匀指的就是这种等可能性。

落在某一点的概率都是相同的

若[x1,x2]是[a,b]的任一子区间，则

P{x1≤x≤x2}=(x2-x1)/(b-a)

这表明X落在[a,b]的子区间内的概率只与子区间长度有关，而与子区间位置无关。

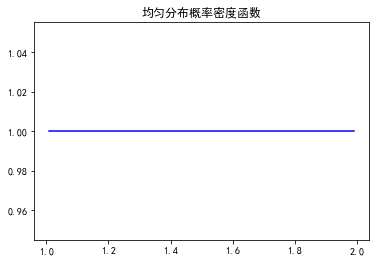
fig,ax = plt.subplots(1,1)

loc = 1
scale = 1

#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = uniform.stats(loc,scale,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时，ppf就是p(X<x)=0.01时的x值。
x = np.linspace(uniform.ppf(0.01,loc,scale),uniform.ppf(0.99,loc,scale),100)
ax.plot(x, uniform.pdf(x,loc,scale),'b-',label = 'uniform')

plt.title(u'均匀分布概率密度函数')
plt.show()

 6、指数分布X~ E（λ）

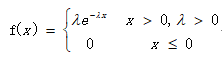
 E = 1/λ

 D = 1/λ^2

fig,ax = plt.subplots(1,1)

lambdaUse = 2
loc = 0
scale = 1.0/lambdaUse

#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = expon.stats(loc,scale,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时，ppf就是p(X<x)=0.01时的x值。
x = np.linspace(expon.ppf(0.01,loc,scale),expon.ppf(0.99,loc,scale),100)
ax.plot(x, expon.pdf(x,loc,scale),'b-',label = 'expon')

plt.title(u'指数分布概率密度函数')
plt.show()

　　

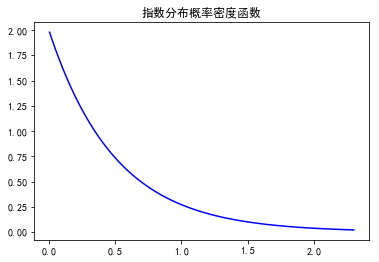
 指数分布通常用来表示随机事件发生的时间间隔，其中lambda和poisson分布的是一个概念（我认为），不知道为什么知乎上：https://www.zhihu.com/question/24796044，他们为啥说这俩不一样呢？我觉得这两种分布的期望肯定不一样啊，一个描述发生次数，一个描述两次的时间间隔，互为倒数也是应该的啊。

指数分布常用来表示旅客进机场的时间间隔、电子产品的寿命分布（需要高稳定的产品，现实中要考虑老化的问题）

指数分布的特性：无记忆性

比如灯泡的使用寿命服从指数分布，无论他已经使用多长一段时间，假设为s，只要还没有损坏，它能再使用一段时间t 的概率与一件新产品使用时间t 的概率一样。

这个证明过程简单表示：

P(s+t| s) = P(s+t , s)/P(s) = F（s+t）/F（s）=P(t)

7、正态分布（X~N(μ，σ^2)）

 

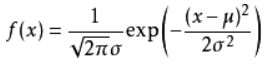
E = μ

D = σ^2

 正态分布是比较常见的，譬如学生考试成绩的人数分布等

fig,ax = plt.subplots(1,1)


loc = 1
scale = 2.0
#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = norm.stats(loc,scale,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时，ppf就是p(X<x)=0.01时的x值。
x = np.linspace(norm.ppf(0.01,loc,scale),norm.ppf(0.99,loc,scale),100)
ax.plot(x, norm.pdf(x,loc,scale),'b-',label = 'norm')

plt.title(u'正太分布概率密度函数')
plt.show()

　　

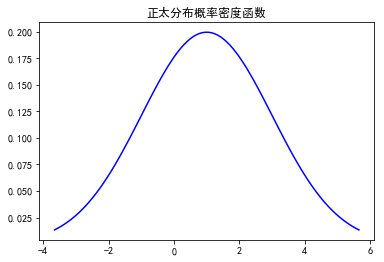
补充：

大数定理：

随着样本的增加，样本的平均数将接近于总体的平均数，故推断中，一般会使用样本平均数估计总体平均数。

 大数定律讲的是样本均值收敛到总体均值

中心极限定理：

独立同分布的事件，具有相同的期望和方差，则事件服从中心极限定理。他表示了对于抽取样本，n足够大的时候，样本分布符合x~N(μ,σ^2)

中心极限定理告诉我们，当样本量足够大时，样本均值的分布慢慢变成正态分布