(学习12)点着色问题

问题描述:

图的m着色问题。给定无向连通图G和m种颜色，用这些颜色给图的顶点着色，每个顶点一种颜色。如果要求G的每条边的两个顶点着不同颜色。给出所有可能的着色方案；如果不存在，则回答“NO”。

问题解析:

设无向图的邻接矩阵为,从1开始，P_i代表点i

0 1 1 1 0

1 0 1 1 1

1 1 0 1 0

1 1 1 0 1

0 1 0 1 0

 

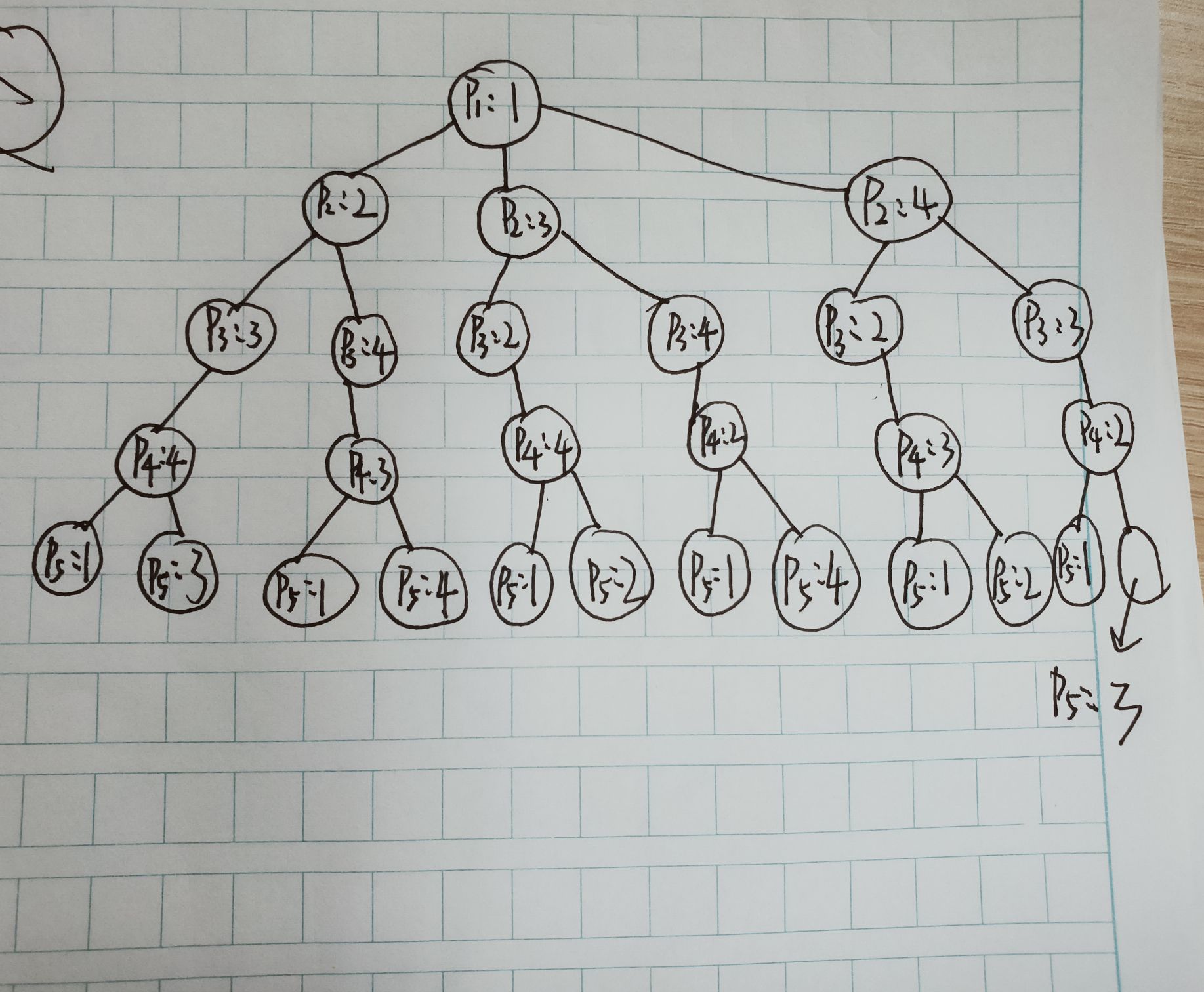
这是解析点一取1的情况，其他的情况的绘制与此相似，都是有12种方案，故最后总方案数48，故不做赘述。

代码设计:

//
//  main.cpp
//  作业12
//
//  Created by yizhihenpidehou on 2020/5/26.
//  Copyright © 2020 yizhihenpidehou. All rights reserved.
//

#include <iostream>
#include <stdio.h>
int graph[100][100];//记录无向图
int color[100];//记录颜色
int count;
int n,m;;//点数，颜色数
int check(int num){//检查每两个点之间是否着色不同
    for(int i=1;i<=num;i++){//检查前个点与当前点的颜色是否冲突
        if(graph[num][i]==1&&color[i]==color[num]){//两点相连并且着色相同，则冲突
            return 0;
        }
    }
    return 1;
}
void graphColor(int num){//着色
    if(num==n+1){
        for(int i=1;i<=num;++i){//输出方案
            printf("%d ",color[i]);
        }
        printf("
");
        count++;
        return ;
    }
    else{
        for(int i=1;i<=m;i++){
            color[num]=i;//先着色
            if(check(num)){//测试当前颜色是否冲突
                graphColor(num+1);//继续向下着色
            }
            color[num]=0;//回溯
        }
    }
}
int main(int argc, const char * argv[]) {
    scanf("%d %d",&n,&m);
    for(int i=1;i<=n;i++){//输入连通图
        for(int j=1;j<=n;j++){
            scanf("%d",&graph[i][j]);
        }
    }
    printf("
");
    graphColor(1);
    if(count==0){//不存在方案
        printf("NO
");
    }
    else{
        printf("num:%d
",count);//输出方案数
    }
    return 0;
}

复杂度分析:

由于对每个点的着色要区分m种情况，并且根据该点的情况要对其他的点的着色进行检测冲突以及考虑着色情况，若发生着色冲突，则回溯,故时间复杂度为O(mn²)