POJ-3581 Sequence(后缀数组)

题意:给定N个数字组成的序列(A_1, A_2, ..., A_n)。其中(A_1)比其它数字都大。现在要把这个序列分成三段，并将每段分别反转，求得到的字典序最小的序列是什么？要求分得的每段都不为空。

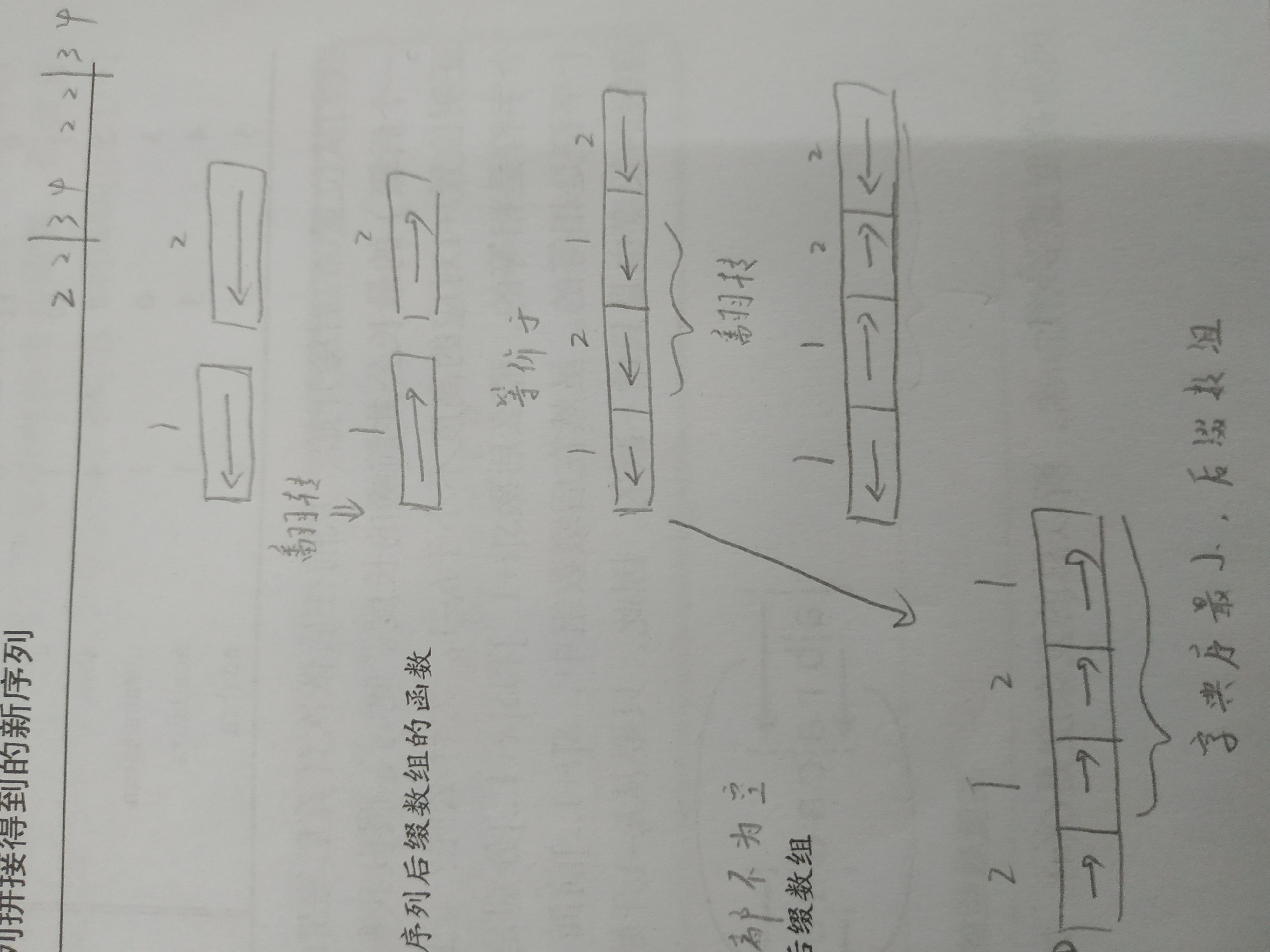
分析:首先确定第一段的分割位置。这很好说，由于(A_1)比其它数字都大，确定第一段的分割位置只需要考虑第一段就足够。将这个字符串反转之后，求反转后的字符串的字典序最小的后缀。重要的是后面的段，这两部分不独立。根据白书的讲解，我们可以得到如下的图，这样就清晰了

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <string>
#include <algorithm>

using namespace std;
const int N = 200005;
const int inf = 0x3f3f3f3f;
int a[N], n, k;
int rev[2 * N], sa[2 * N];
int rk[2 * N], tmp[2 * N];

bool compare_sa(int i, int j)
{
	if (rk[i] != rk[j]) return rk[i] < rk[j];
	else
	{
		int ri = i + k <= n ? rk[i + k] : -1;
		int rj = j + k <= n ? rk[j + k] : -1;
		return ri < rj;
	}
}

void construct_sa(int s[], int n, int sa[])
{
	for (int i = 0; i <= n; ++i)
	{
		sa[i] = i;
		rk[i] = i < n ? s[i] : -inf;
	}

	for (k = 1; k <= n; k *= 2)
	{
		sort(sa, sa + n + 1, compare_sa);
		tmp[sa[0]] = 0;
		for (int i = 1; i <= n; ++i)
		{
			tmp[sa[i]] = tmp[sa[i - 1]] + (compare_sa(sa[i - 1], sa[i]) ? 1 : 0);
		}
		for (int i = 0; i <= n; ++i)
		{
			rk[i] = tmp[i];
		}
	}	
}

void solve()
{
	//将a反转，并计算其后缀数组
	reverse_copy(a, a + n, rev);
	construct_sa(rev, n, sa);

	int p1;
	for (int i = 0; i < n; ++i)
	{
		p1 = n - sa[i];
		if (p1 >= 1 && n - p1 >= 2) break;
	}

	int m = n - p1;
	reverse_copy(a + p1, a + n, rev);
	reverse_copy(a + p1, a + n, rev + m);
	construct_sa(rev, 2 * m, sa);

	int p2;
	for (int i = 0; i <= 2 * m; ++i)
	{
		p2 = p1 + m - sa[i];
		if (p2 - p1 >= 1 && n - p2 >= 1) break;
	}
	reverse(a, a + p1);
	reverse(a + p1, a + p2);
	reverse(a + p2, a + n);
	for (int i = 0; i < n; ++i) printf("%d
", a[i]);
}


int main()
{
	scanf("%d", &n);
	for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
	solve();
	
	return 0;
}