学习笔记——树上前缀和（模板）

Update 2020.10.6 删除赘余&第二种前缀和修改错误

Update 2021.8.4 美化版面

树上前缀和分两种：

1.从根向下，到某点的前缀和就是从根到这一点的这条路径上点（或者边）的权值之和

如果看着文字很难理解(雾），那我先放出一张我画的图（丑）

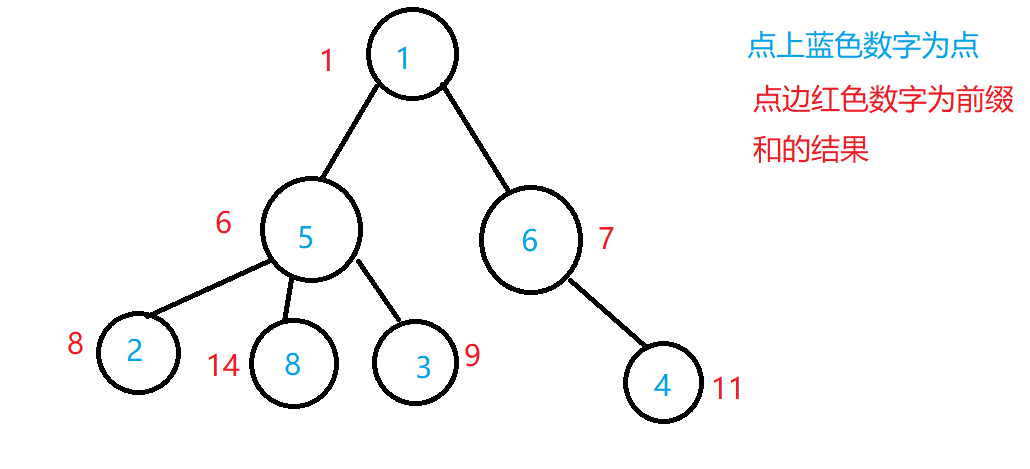
所以解法也很简单，从根开始DFS,向下搜，在搜的过程中累加，就可以了。

如果是边权的情况，那么就把边权给移到儿子节点上，根节点点权为0，当点权来写。

我们令 \(total[i]\) 表示第 \(i\) 号节点的前缀和，

则根节点前缀和就是本身（如果为边权的话就是0）。

再DFS从根向下搜，每次遍历每一个儿子节点之前加一句

total[temp]=ed[i].sum+total[xx]; 
dfs(temp);

类似数组前缀和思想。其中 \(temp\) 就是 \(xx\) 的儿子节点，用邻接表存，\(ed[i].sum\) 就是 \(i\) 号节点的权值（或者是它的父亲节点到它这条边上的权值）

所以只要在DFS时加上那句话就结束了。

code:（以一号节点为根，无向边，有根树，以有边权为例）

#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
using namespace std;
const int N=200005;
const int M=25;
int Q,n,m,head[N],cnt,b[N],k,total[N];
struct node{//采取邻接表存储
    int u,v,next,sum;
}ed[N]; 
void add_edge(int u,int v,int k)
{
    cnt++;
    ed[cnt].u=u;
    ed[cnt].v=v;
    ed[cnt].next=head[u];
    ed[cnt].sum=k;
    head[u]=cnt;
}
void dfs(int xx)
{
    for(int i=head[xx];i!=0;i=ed[i].next)
    {
        int temp=ed[i].v;
        if(b[temp]==0)
        {
            b[temp]=1;
            total[temp]=ed[i].sum+total[xx];
            dfs(temp);
        }
    }
}
int main()
{
    cin>>n;
    for(int i=1;i<n;i++)//n个点，n-1条边
    {
        int x,y,k;
        scanf("%d%d%d",&x,&y,&k);//表示连接x,y有权值为k的边
        add_edge(x,y,k);
        add_edge(y,x,k);
    }
    b[1]=1;
    dfs(1);
    cin>>m;//m次询问前缀和
    while(m--)
    {
        int x;
        scanf("%d",&x);
        cout<<total[x]<<endl; 
    }
    return 0;
} 

2.从底向上，某一点的前缀和就是以那个点为根的一棵子树上所有点权（或边权）之和。

再放一张画图用来描述：

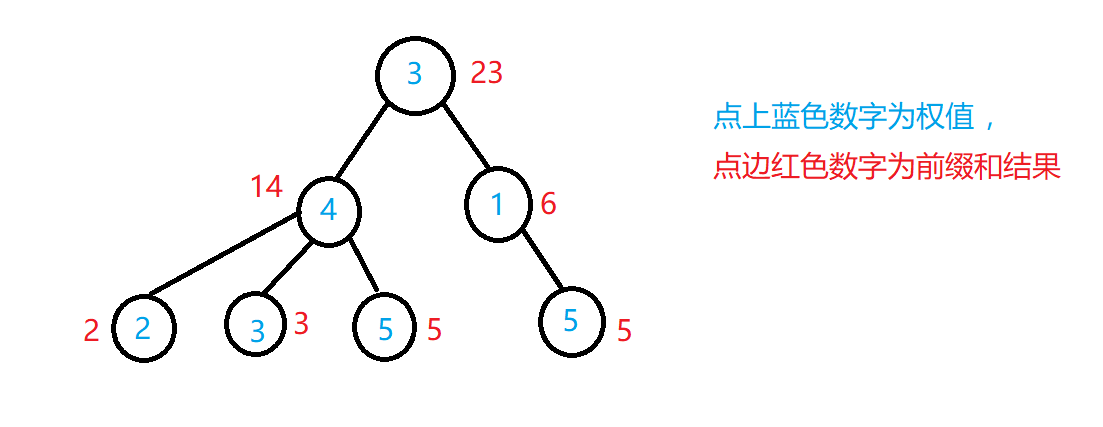
如图，很明显，每个点的前缀和就是以它的所有儿子为根的子树权值和之和。

如果是边权的情况，那么就把边权给移到儿子节点上，根节点点权为0，当点权来写。

我们可以发现，没有儿子节点的前缀和就是它本身

在搜完回溯的时候再加回去就行了，与第一种写这句话的位置有区别

dfs(temp);
total[xx]+=total[temp];

并且，一开始，需要预处理出那些没有儿子节点的点，将它们的前缀和赋为自己本身

for(int i=2;i<=n;i++)//因为以一号节点为根的，所以1号节点必有儿子节点，从2号开始扫）
{
	if(out[i]==1)//在输入时处理出度，如果出度为1，表明这个点只有一条跟别的点连接的边，则这个点一定没有儿子节点
	{
		total[i]=ed[i].sum;//赋值
	} 
} 

code:（以一号节点为根，无向边，有根树，以有边权为例）

#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
using namespace std;
const int N=200005;
const int M=25;
int n,head[N],cnt,dep[N],k,total[N],b[N],out[N];
struct node{
	int u,v,next,w;
}ed[N]; 
void add_edge(int u,int v,int k)
{
    cnt++;
    ed[cnt].u=u;
    ed[cnt].v=v;
    ed[cnt].next=head[u];
    ed[cnt].w=k;
    head[u]=cnt;
}
void dfs(int xx)
{
	for(int i=head[xx];i!=0;i=ed[i].next)
	{
		int temp=ed[i].v;
		if(b[temp]==0)
		{
			b[temp]=1;
			dfs(temp);
			total[xx]+=total[temp];//一定要在dfs结束时前缀和！
		}
	}
}
int main()
{
	cin>>n;
	for(int i=1;i<n;i++)
	{
            int x,y,k;
            scanf("%d%d%d",&x,&y,&k);
            add_edge(x,y,k);
            add_edge(y,x,k);
		out[x]++;//出度的预处理，无向图，所以双向处理出度+1
		out[y]++; 
	}
	total[1] = ed[1].w;//根要单独处理
	for(int i=2;i<=n;i++)
	{
		if(out[i]!=1)
		{
			total[i]=ed[i].w;//将所有不为叶子的节点，全赋上那个点的初值(因为是边权，都放到了父亲节点)
		} 
	} 
	b[1]=1;
	dfs(1);
	int m;
	cin>>m;
	while(m--)
	{
		int x;
		cin>>x;
		cout<<total[x]<<endl;
	} 
	return 0;
}

如果您还学过一些LCA，那您可以做一下LOJ#10130，简单的应用