22. Generate Parentheses

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

For example, given n = 3, a solution set is:

"((()))", "(()())", "(())()", "()(())", "()()()"

特殊的姿势进行dfs

心中有树就能写好dfs

class Solution {
public:
    void dfs(int n,string s,int x,int y,vector<string>&v){
        if(y==n){
            v.push_back(s);
            return ;
        }
        if(x<n)dfs(n,s+'(',x+1,y,v);
        if(x>y)dfs(n,s+')',x,y+1,v);
    }
    vector<string> generateParenthesis(int n) {
        vector<string>v;
        string s="";
        dfs(n,s,0,0,v);
        return v;
    }
};

x表示左括号的数量,y表示右括号的数量。......反正也没人看自己看 就随便写写吧。

原问题可以转换成求 (0,0)到(n,n) 路径。条件得满足x>=y

如果加一个左括号(0,0)->(1,0)  再加一个 右括号(1,0)->(1,1)

那么最终 能得到的合法序列就是一条从(0,0)到(n,n)的路径，我们把这条路径就录下来就可以了。

为了方便理解  上个图

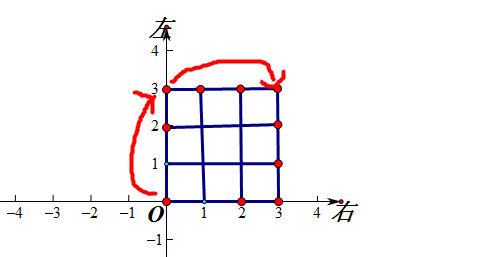
如图 红线标记的路径，向上走一步添加一个左括号，向右走一步添加一个右括号。