P2342 叠积木

　　带权并查集——今天写真有些新的体会。

　　我画了个图：

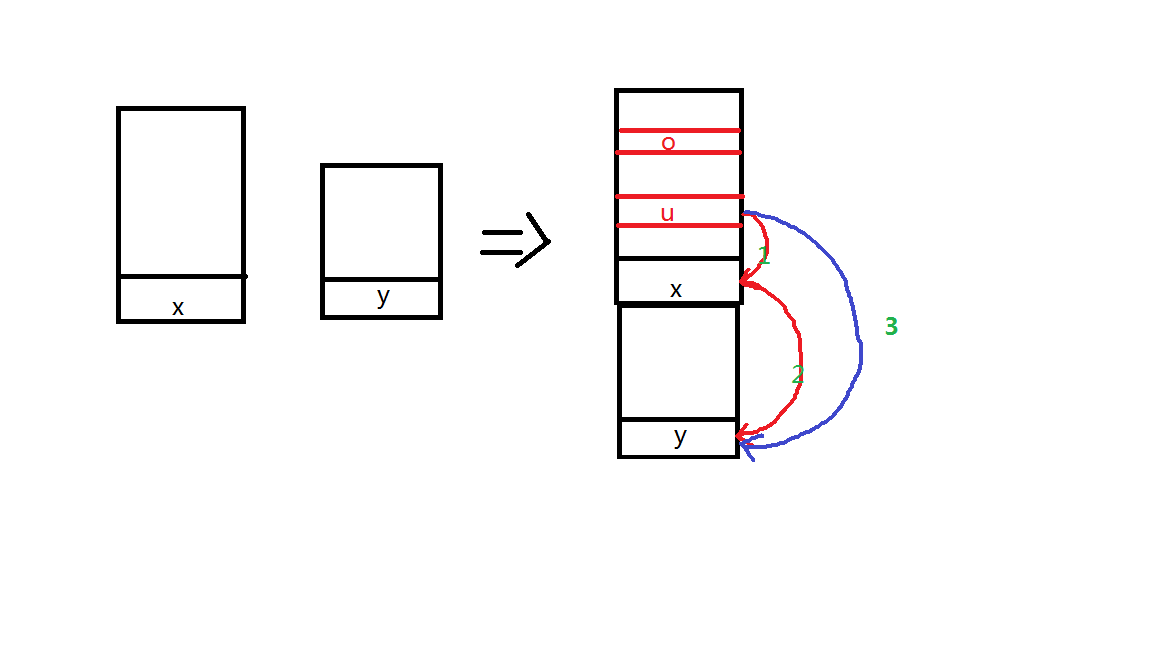
　　比如说，我们现在要将x移动到y上，我们维护 fa [ x ] 表示这一堆最下面的那个，那么我们先这样：

        fa[x]=y;    
    dep[x]=sz[y];
    sz[y]+=sz[x];

　　之后再要求比如说 o 的深度的时候，我们：

scanf("%d",&a);
find(a);
printf("%d
",dep[a]);

　　find的代码如下： 

int find(int x)
{
    if(x==fa[x]) return x;
    int FA=find(fa[x]);
    dep[x]+=dep[fa[x]];
    return fa[x]=FA;
}

　　也就是说，每一次我都加上路径压缩前的 fa [ x ] 的深度，再路径压缩。

　　在那个图上，就是这样的过程：

　　u找到x，x找到y，回溯，x加上y的深度，还是x，而在两个合并的时候x的深度就已经改成y的大小了，所以x本来就不用改了；再回溯，u的深度加上x的深度，也就是y的大小，之后很重要——u的父亲被改成y，就保证了第二次问u直接就能找到y，那么加上0还是u，保证了u不再改变。

　　如果再找o，也是先到x，再到y，改o的父亲。

　　也就是说，形象地理解：x就像一个一次性的中转站，对于原来每一个x的孩子，再被第一次询问的时候都要经过x，再他们的新父亲，而当他们到原来的父亲（x）的时候，贡献就被加上了，并且只会被加一次，之后，被询问的儿子们要是再次被询问，就会直接找到新的父亲（y）了。

　　真的，挺好……　　

　　完整代码time——

#include<cstdio>
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
#include<vector>
using namespace std;
#define maxn 300005
int fa[maxn],sz[maxn],dep[maxn];
int n;
int find(int x)
{
    if(x==fa[x]) return x;
    int FA=find(fa[x]);
    dep[x]+=dep[fa[x]];
    return fa[x]=FA;
}
void merge(int x,int y)
{
    x=find(x);
    y=find(y);
    if(x==y) return ;
    fa[x]=y;
    dep[x]=sz[y];
    sz[y]+=sz[x];
}
int main()
{
    for(int i=1; i<=30000; i++)
    {
        fa[i]=i;
        sz[i]=1;
        dep[i]=0;
    }
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        char s;
        int a,b;
        cin>>s;
        if(s=='M')
        {
            scanf("%d%d",&a,&b);
            merge(a,b);
        }
        else
        {
            scanf("%d",&a);
            find(a);
            printf("%d
",dep[a]);
        }
    }
    return 0;
}