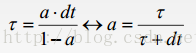The Balance Filter

互补滤波 Shane Colton<sconlton@mit.edu> June 25,2007

应用于平衡平台的加速度和角速度测量值融合的一种简单的解决方案。

传感器

 

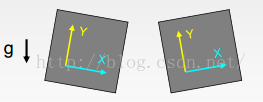
2轴加速度计：

• 测量“加速度”，实际上是每单位质量所受到的力（F=ma,所以a=F/m）；
• 可以用来测量重力，如上图所示，X轴为0，Y轴为-1g；
• 可以用来测倾角：

 

X轴方向有了重力的分量，左侧是正分量，右侧是负分量。Y方向上比重力小了一些。

Y方向有有用的信息吗？可能并没有：

a)在角度信息上来说，Y方向上没有X方向上敏感；

b)不能反映倾角的方向。

 

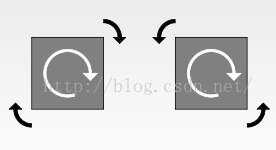
陀螺仪：

• 测量角速度（旋转的速度）
• 静止的时候为0
• 旋转的时候为正或者负

左侧为正，右侧为负。

 

从传感器中读取数据

首先是读取每一个传感器的模拟输入（通过模数转换器ADC）并把它们变成有用的单位。这需要两个量补偿和比例：

1、补偿很容易得到：观察水平或者静止时候的传感器值，如果这个值有噪声，取平均值。这个补偿应该是一个

有符号的整型变量（或者常量）。（尽管ADC的值和补偿都不是负的，但是它们将会做减法，所以现在让它是一

个有符号变量是没有大碍的。）

2、比例取决于传感器：它是一个为了得到期望单位的乘法因子（陀螺仪每秒的单位可以是度也可以是弧度，只

要单位统一就好）。这可以在数据手册中找到或者通过实验确定，有时候称之为常量、增益或者敏感度。这个比

例应该是一个浮点型变量或者常量。

 

关于加速度计的更多…

    如果需要对360的旋转进行角度测量估计，而这是必要的，Y轴的测量是有用的但是并非必须。有它，我们可以使用三

角函数来求出两个轴的反正切并计算出角度；没有它，我们仍然可以使用sin或者cos找出和X轴之间的夹角，因为我们知道

重力的大小。但是三角函数的计算需要大量的处理时间，而且是非线性的，所以能够避免不用就应该避免。

    对于一个平衡平台来说，最重要的需要测量的角度几乎是接近垂直的。因为如果平台向任何方向倾斜超过30度，处理

器除了尽全力去试图扳回它外，可能干不了什么了。所以在这个范围内，我们可以采用小角度近似而且计算X轴方向可以

减轻处理器负担和代码复杂程度。

 

假设平台向某个方向倾斜，角度为Θ，保持静止（没有垂直方向上的加速度）

X轴方向：1g*sinΘ

小角度近似：sinΘ=Θ（弧度值）

在5%范围内（相当于Θ=±π/6=±30°），效果良好。

所以有如下代码：

x_acc=(float)(x_acc_ADC-x_acc_offset)*x_acc_scale;

且如果x_acc_scale是比例缩放到1g，同时x轴方向为垂直向下，x_acc将是以弧度做单位的角度值。如果想要得到以度为单

位的角度，x_acc_scale应该乘以180/π。

理想的测量

    为了控制平台，能得到它的角度和角速度将是最好的。这是角度的PD（比例微分）控制的基础，而PD对于这样的系

统来说效果良好。

    电机输出=Kp×（角度）+Kd×（角速度）

    电机输出具体是怎样的，这里就不阐述了。但是通常来说控制程序可以通过Kp和Kd的调节得到稳定平滑的性能效果。

不会产生纯比例控制器那样的过冲。（比如说如果角度为正，而角速度为负，在返回水平位置的过程中，电机会提前减

速。）

从效果上来说，PD控制器就像加上了一个可调弹簧和阻尼器。

传感器图

最好的方法是？

最明显的方法

 

    优点：

• 直观
• 编程简单
• 陀螺仪反应迅速，可准确快速的角速度测量

    缺点：

• 噪声
• 任何水平方向上的加速度的变化都会影响角度（想象平台是水平的，但是电机让它向前运动，加速度计将
• 不能把它和重力分开。）

快速粗糙的滤波

    优点：

• 依然直观
• 依然编程方便
• 滤波器滤去高频的水平加速度（噪声），只有低频的加速度（重力）可以输出

    缺点：

• 角度的测量由于取平均将会出现延迟，滤波越多，延时越长。延时将会对稳定性产生影响。

单传感器方法

    优点：

• 只有读取一个传感器
• 快速，延迟不是问题
• 不受水平加速度的影响
• 依然编程易实现

    缺点：

• 严重的陀螺仪漂移。如果陀螺仪静止的时候没有准确的校零（确实不会），它将会慢慢的漂移直到误差越
• 来越大。

卡尔曼滤波

    

    优点：

• 理想的滤波器可以融合带有噪声的传感器，并得到干净准确的估计
• 考虑已知系统的物理属性（质量、惯性等等）

    缺点：

• 我不知道它是如何工作的，数学上很复杂，需要一些线性代数的知识。而且不同的情况有不同的形式
• 可能很难编程
• 增加处理器负担

互补滤波器

优点：

• 有助于解决噪声、漂移和水平方向上的加速度分离的问题
• 快速估计，比单独的低通滤波快
• 不是很耗处理器时间

缺点：

• 相对于简单的滤波器，这里有一点理论，但是对于卡尔曼滤波器来说，什么都不是

数字滤波器的更多

在数字滤波器这方面有大量的理论，大多数我都不懂。没有理论基础（Z域的变换，如果你想多看看的话），但

是基本的概念还是很简单的。

 

积分：这个很简单。想象一个以已知速度运行的汽车，你的程序就像一个一毫秒数一次的时钟。每次为了得到新

的距离，你在上一次的距离上加上改变量。改变量等于车速乘以从上次到现在的时间，这个时间你可以从控制器

上得到或者来自其他已知的定时器。

距离+=速度*dt;对于我们的平台来说是，angle+=gyro*dt;

 

低通滤波器：低通滤波器的目标只是为了让低频的改变通过，滤掉高频的噪声波动。实现它的一种方法是在程序

的循环中一点一点的加。

angle=0.98*angle+0.02*x_acc;

比如，如果角度从零开始改变，加速度的值突然跳到10°，在随后的迭代过程中，角度的估计将会如下表所示

如果角度保持在10°，这个角度的估计将会上升到和这个值持平，到达这个值的时间取决于滤波器常数（例子中的

0.98和0.02）和循环中的采样率dt

高通滤波器：相对于低通滤波器来说，理解上要难一些，但是理论上来说它俩是完全相反的：它允许高频信号通过，

滤去一直保持不变的信号，这可以有效的解决漂移的问题。

采样周期：每个循环的时间。如果采样频率是100Hz，采样周期是0.01秒。

时间常数：滤波器的时间常数和滤波信号的持续时间相关。对于低通滤波器来说，比时间常数更长的信号将会保持

不变，而比时间常数短的信号将会被滤掉。高通滤波器完全相反。一个数字低通滤波器的常数τ：

y=a*y+(1-a)*x;

以采样周期dt运行的循环，如下：

所以如果已知期望的时间常数和采样频率，可以得到滤波器系数a。

互补：这只是说滤波器有两部分组成，以得到准确线性的估计。在阅读相关的更多的东西之后，我认为这里的滤波

器不仅仅是互补，在时间常数比采样频率更大的时候，这是一个很好的近似。

细瞥角度互补滤波器

如果这个滤波器以每秒执行100次的循环中运行，低通高通滤波器的时间常数都将会是

    这定义了信任陀螺仪和加速度计的界限。对于时间周期小于半秒，陀螺仪的积分将会优先，水平加速度的噪

声将会被滤去。对于时间周期长于半秒，加速度的均值相对于陀螺仪来说占得比重更大一些，这个时候可能会有

一些漂移。

    对于绝大部分来说，设计滤波器通常以另一种方式进行。首先，取一个时间常数，然后用它来计算滤波器系

数。取得这个时间常数应可以满足系统的响应。如果陀螺仪每秒钟漂移2°（可能是非常糟糕的估计了），时间

常数可能需要小于一秒，以保证每秒钟在任何方向上漂移度数不会超过两度。但是时间常数越低，允许水平方向

加速度噪声通过的就越多。就像大多数控制算法面临的状况一样，这里有一个平衡点，唯一的办法就是实验调试。

    为了选择正确的滤波器系数，记住这个采样频率是很重要的。如果修改程序，加上了更多的浮点运算，采样

频率将要下降两倍，时间常数应该上升两倍，除非你重新计算滤波器系数。

    举一个例子，考虑使用26.2ms的速度更新控制周期（可能有点慢，但是还能用）。如果想要得到0.75s的时间

常数，滤波器系数应该是

所以有

第二个滤波器参数为1-0.966=0.034.

    滤波器里面的陀螺仪没有准确校零的问题值得探讨一下。它完全不会导致漂移的问题，但是会影响角度的计算

。举个例子，我们错误地选择了一个不正确的补偿，陀螺仪静止的时候，得到的值是5°/s。在数学上可以证明（这

里就不证明了），这在角度估计的影响就是补偿率乘以时间常数。所以如果我们取0.75s的时间常数，将会得到3.75°

的角度补偿常量。

除了这个非常糟糕的情况（陀螺仪永远不会需要那么大的补偿），角度补偿常量比漂移角度补偿简单得多。比如你可

以反方向旋转3.75°来解决这个问题。

理论足够了，是时候看看实验的效

果了。

*http://www.machinescience.org

采样频率：79Hz

滤波器系数：0.98和0.02

时间常数：0.62s

注意滤波器是如何处理这两个问题的：在不旋转的时候水平方向上的加速度干扰（蓝色高亮）和陀螺仪漂移

（红色高亮）

 

采样频率：84Hz

滤波器系数：0.98和0.02

时间常数：0.58s

这里有两点值得注意：第一，没有考虑到的启动的问题（蓝色高亮），这将发生在你没有合适的初始化你的变量

时。长的时间常数意味着开始几秒是不确定的，这很容易解决：确保重要的变量都准确的初始化了（0或者其他

应该是的值）；第二，注意苛刻的陀螺仪补偿（红色高亮），大约6°/s，注意是如何在角度估计里面产生角度

补偿常量的。补偿的角度约等于陀螺仪补偿乘以时间常数。这是一个很好的最坏情况分析。

总结

我认为这个滤波器很适合DIY平衡解决方案，理由如下：

• 效果不错。角度估计是可靠而准确的，没有水平加速度干扰问题和漂移问题。
• 处理器友好性。只需要很小的浮点运算量，稍微修改一下代码即可应用到你的程序中。很容易实现控制周
• 期达到100Hz。
• 它更加的直观，理论也更加容易阐释相对于替代品卡尔曼滤波来说。This might not have anything to 
• do with how well it works, but in educational

programslike FIRST, it can be an advantage.（在入门教育中这很有优势）。

    在我说对于平衡平台是一个完美的解决方案之前，我很看看他在一些硬件平台上的测试，比如DIY Segway？

    我不确定它应用到水平定位上表现如何。我不太怀疑：没有重力，加速度计不能给绝对参考，，当然可以积

分两次以得到位置估计，但是漂移会很严重。尽管滤波的技术可以用不同的传感器互相补偿（可能是加速度计和

编码器），但是工况是类似的（编码器不是绝对位置的设备，如果轮子失去牵引力，也会漂移）。使用水平位置

的一个更好的类比是使用GPS做长时间的估计，惯性传感器做短期集成。