[每日一题]:Shortest Path(NowCoder)

题目:

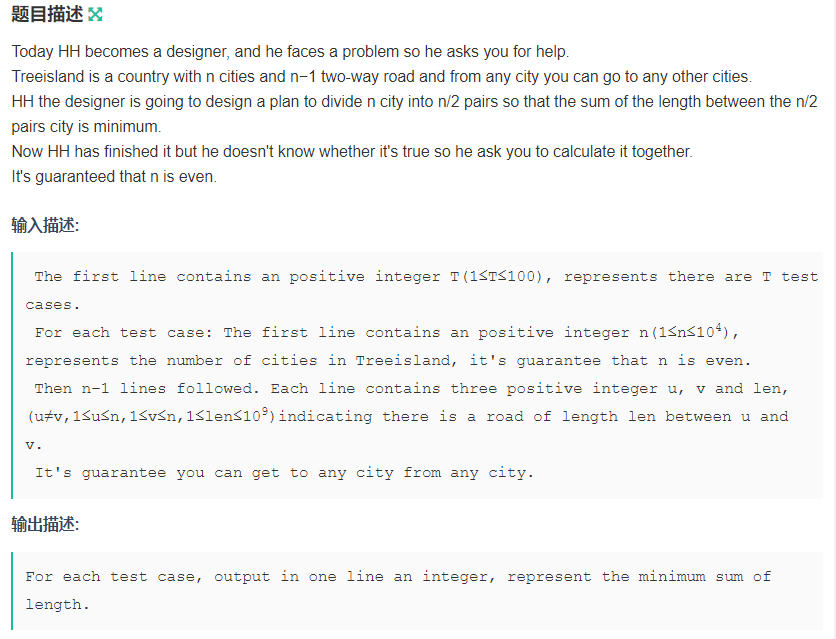
题目大意:

 给你一颗树,然后将 n (n 确保是偶数) 个点 分成 n / 2 对,使得这 n / 2 对之间的路径长度之和最小。

析题得侃:

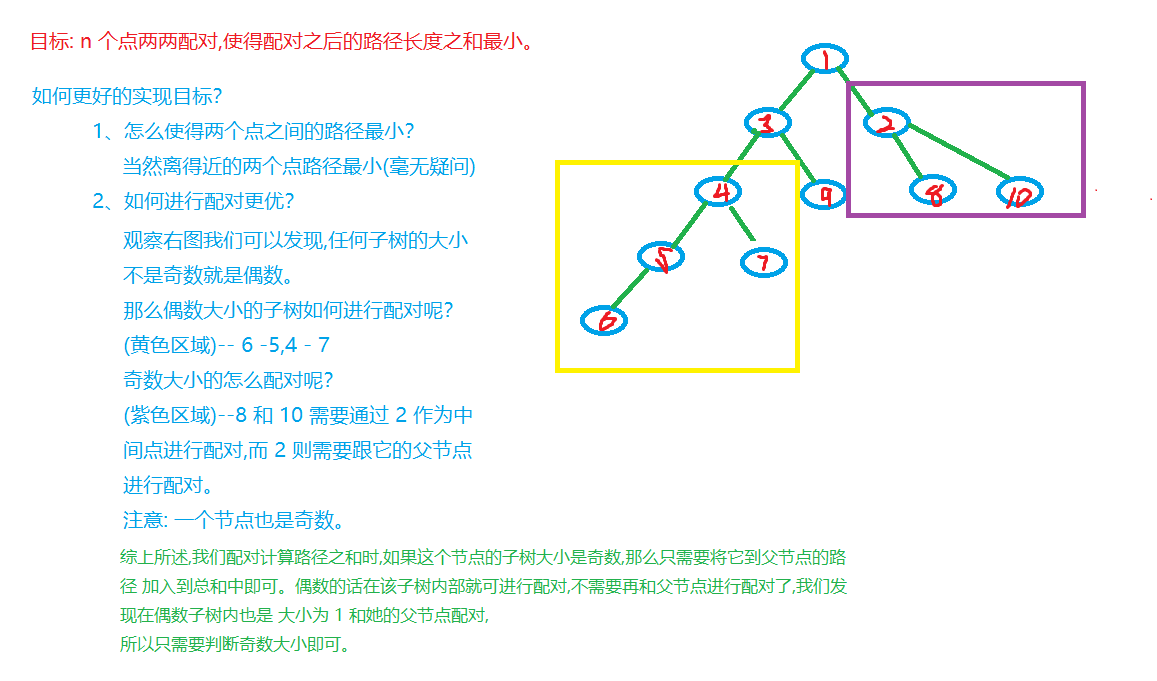
Code:

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 2e5 + 10;
typedef long long LL;
// 建反向边一定要开 2 倍空间 
int head[maxn],Next[maxn],edge[maxn],ver[maxn];
int size[maxn];

int t,n,tot;
int u,v,w;

LL res = 0;

void add(int u,int v,int w) {
    ver[++ tot] = v,edge[tot] = w;
    Next[tot] = head[u],head[u] = tot;
    return ;
}

void DFS(int s,int fa,LL sum) {
    for(int i = head[s]; i; i = Next[i]) {
        int y = ver[i];
        if(y != fa) {
        	// 我们传的权值只需要是 该节点到子节点大小即可 
            DFS(y,s,edge[i]);
            // 是当前节点的总大小,所以应该加上 所有子节点的大小 
            size[s] += size[y];
        }
    }
    // 判断节点大小是否是 奇数 
    if(size[s] & 1) res += sum;
    return ;
}

int main(void) {
    scanf("%d",&t);
    while(t --) {
    	// 多组测试,一定要记得初始化 
    	tot = 0;
    	memset(head,0,sizeof(head));
        scanf("%d",&n); 
        for(int i = 1; i <= n; i ++) {
            size[i] = 1;
        }
        for(int i = 1; i < n; i ++) {
          scanf("%d%d%d",&u,&v,&w);
            add(u,v,w);
            add(v,u,w);
        }
        res = 0;
        DFS(1,-1,0);
        printf("%lld
",res);
    }
    return 0;
}