java数据结构--线性表

一、线性表基本概念

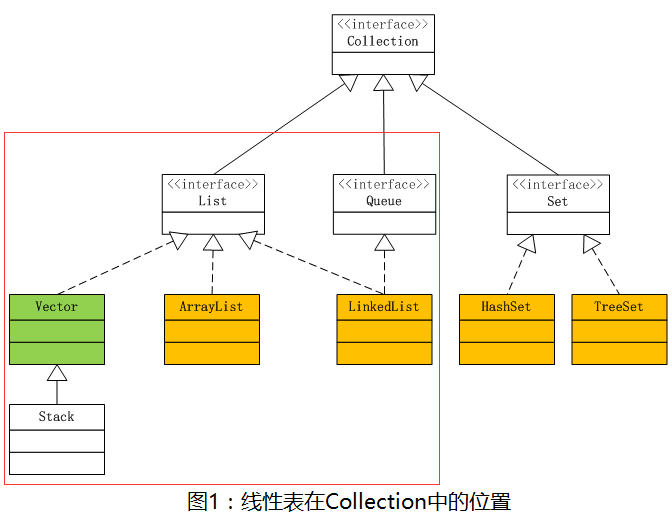
线性表是其组成元素间具有线性关系的一种线性结构，是由n个数据类型相同的元素构成的有限序列。其具有“一对一”的逻辑关系，与位置有关，除了头尾元素之外，每一个元素都有唯一的前驱元素和后继元素，即元素ai前面的元素为ai-1，后面的元素为ai+1。

  

二、顺序表

1、概念

顺序存储指用一组地址连续的存储单元 依次存放 线性表中的数据元素的存储结构。用顺序存储的线性表就称为顺序表，所有数据元素的存储位置均取决于第一个数据元素的存储位置。

2、特点

• 逻辑上相邻的数据元素，赋以相邻的存储位置；

• 存储密度高；

• 便于随机存取；

• 不便于插入、删除操作。

   

  3、描述

  常使用数组作为顺序表的底层数据结构进行存储。

代码实现

package 顺序表;

/**
 * @author psy
接口
 */
public interface IList {
    public void insert(int index,Object data) throws Exception;        //在指定位置插入元素
    public void clear();    //清空线性表
    public void remove(int index);    //删除指定位置元素
    public boolean isEmpty();        //判断线性表是否为空
    public Object get(int index);    //获取指定位置元素
    public int length();            //获取线性表长度
    public int indexOf(Object data);//获取指定元素的角标
    public void display();            //输出线性表中所有元素

}

package 顺序表;

/**
 * @author psy
 * 优点：存取元素快；
 * 缺点：插入和删除元素慢，且需要预先分配空间，容易造成空间不足或空间浪费
 */
public class SqList implements IList {

    private Object[] listItem;        //顺序表的存储空间大小；
    private int curLen;                //顺序表的当前长度
    private int maxSize;            //顺序表的最大尺寸

    //构造最大尺寸为maxSize的顺序表
    SqList(int maxSize){
        this.maxSize = maxSize;
        this.curLen = 0;
        this.listItem = new Object[maxSize];
    }

    //在第index的位置插入数据data
    @Override
    public void insert(int index, Object data) throws Exception{
        if(curLen == maxSize)                    //判断存储空间是否已满
            throw new Exception("数组已满，无法插入！");
        if(index<0||index>curLen)                //判断插入位置是否合法
            throw new IndexOutOfBoundsException("所插入的位置不在索引范围！");
        for(int i=curLen;i>index;i--) {            //将插入位置后面的所有元素后移一位
            listItem[i]=listItem[i-1];
        }
        listItem[index] = data;                    //插入数据
        curLen++;                                //表长+1

    }

    //清空顺序表
    @Override
    public void clear() {
        curLen = 0;//顺序表的当前长度等于0
    }

    //删除顺序表中指定位置index处的数据
    @Override
    public void remove(int index) throws IndexOutOfBoundsException{
        if(index<0||index>curLen)                //判断位置是否合法
            throw new IndexOutOfBoundsException("当前索引不存在！");
        for(int i=index;i<curLen;i++) {            //将指定位置之后的元素均前移一位
            listItem[i] = listItem[i+1];
        }
        curLen--;                                //表长-1
    }

    //判断顺序表是否为空
    @Override
    public boolean isEmpty() {
        return curLen == 0;
    }

    //获取交表为index处的数据
    @Override
    public Object get(int index) throws IndexOutOfBoundsException{
        if(index<0||index>curLen)
            throw new IndexOutOfBoundsException("当前索引不存在！");
        return listItem[index];
    }


    //返回顺序表长度
    @Override
    public int length() {
        return curLen;
    }

    //获取元素在顺序表中的位置
    @Override
    public int indexOf(Object data) {
        for(int i=0;i<curLen;i++) {//如果在数组中找到了就返回这个元素的数组下标
            if(listItem[i] == data)
                return i;
        }
        return -1;//否则返回-1
    }

    //显示顺序表中的元素
    @Override
    public void display() {
        for(int i=0;i<curLen;i++)//遍历
            System.out.print(listItem[i]);
    }
}

package 顺序表;

/**
 * @author psy
 * 我们的ArrayList底层是数组实现的，底层元素在内存中是按顺序排列的，ArrayList是Java中顺序表的体现。
 */
public class Temp {
    public static void main(String[] args) throws Exception{
        SqList list=new SqList(20);
        list.insert(0,"你好");
        list.display();
    }
}

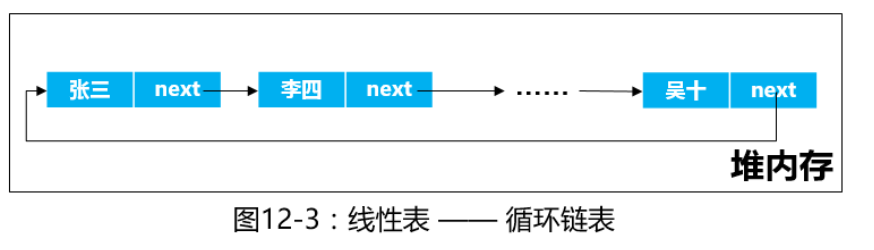
三、链式表

链表在物理存储上通常是非连续、非顺序的方式存储的，数据元素的逻辑顺序是通过链表中的引用来实现的。

1、单链表

在我们平时的使用中，通过数组我们可以快速的存储元素，链表也是和数组一样可以用来存储元素，但是链表在一些方面比数组的效率更高，在查找元素的时候我们通常用数组来存储，但是当我们插入和删除元素的时候，通常我们使用链表来进行操作。链表我们通常定义有两个域：数据域和指针域。数据域存储的是我们要存储的数据，指针域存储的是我们要指向下一个地址的指针。

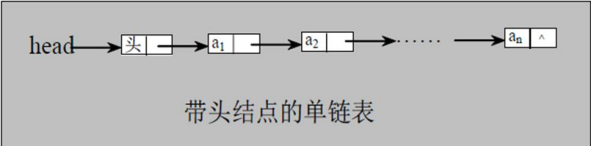
单链表的存储方式如下：

单链表的每个元素的存储空间不是连续的，我们只能通过第一个数据的指针找到下一个元素的位置，之后才能进行访问。这里面在链表中我们通常加一个head(头指针)，这个头指针可以方便我们对链表头元素的插入和删除，它仅仅代表一个标志，里面可以写上链表的长度等等。

 

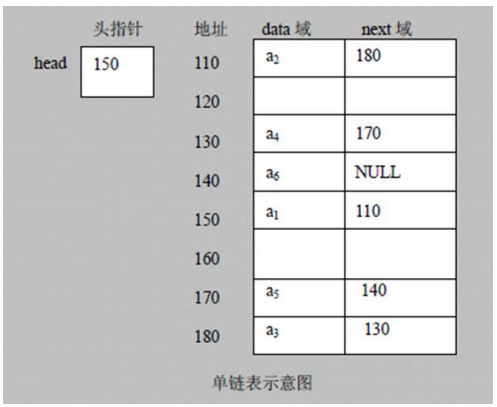
带表头的单链表的逻辑示意图如下：

 

 代码实现

package 单链表;

/**
 * @author psy
 */
public class Node {
    public Node() {

    }

    // 使用构造函数,在构造时就可以给data赋值
    public Node(int data) {
        this.data = data;

    }


    private Node head;// 头节点
    // 这里存的是比较简单的int类型
    public int data;//存放数据的data
    public Node next;//next引用，指向下一个节点
    /**
     * 增加操作
     *
     * @param data
     */
    public void addNode(int data) {
        // 实例化一个节点
        Node newNode = new Node(data);
        // 判断头节点是否为空,如果是空就给他赋值
        if (head == null) {
            head = newNode;
            return;
        }
        // 接收head头指针的对象
        Node temp = head;
        // 遍历单链表,直到遍历到最后一个则跳出循环。
        while (temp.next != null) {
            // 往后移动一个节点,指向下一个节点
            temp = temp.next;
        }
        // temp为最后一个节点或者是头节点,将其next指向新节点
        temp.next = newNode;
    }
    /**
     * @param index:删除第index个节点
     *             删除节点，不是删除下标
     * @return
     */
    public boolean deleteNode(int index) {
        //index小于1或者大于长度，不合法
        if (index < 1 || index > length()) {
            return false;
        }
     int length=1;//记录遍历到哪一个结点了
        Node tmep=head;//可移动的指针
        while (tmep.next!=null){//遍历单链表
            //temp：前一个节点   temp.next：当前节点   temp.next.next：下一个结点
            if (index==length++){
                tmep.next=tmep.next.next;
                return true;
            }
            tmep=tmep.next;//遍历一次往后移一次
        }
        return false;
    }

    /**
     * 返回单链表长度
     *
     * @return
     */
    public int length() {
        int length = 0;
        Node temp = head;
        while (temp != null) {
            length++;
            temp = temp.next;
        }
        return length;
    }

    /**
     * 打印单链表
     */
    public void printList() {
        Node tmp = head;
        while (tmp != null) {
            System.out.println(tmp.data);
            tmp = tmp.next;
        }
    }

}

package 单链表;

/**
 * @author psy
 * 有一个头指针，指向第一个元素的地址
 * 每一个元素有一个数据域和指针域
 * 数据域存放元素对应的数据
 * 指针域对应下一个元素的地址
 */
public class Temp {
    public static void main(String[] args) {
        Node node = new Node();
        node.addNode(1);
        node.addNode(2);
        node.addNode(3);
        node.deleteNode(1);//最后一个节点指向空

        node.printList();
    }
}

3、循环链表

循环链表就是在单链表的基础上修改而来，只是将尾结点的指针域指向了头结点，从而形成一个环状的链表。 在实现循环链表时可以用头指针或尾指针或两者同时使用来标识循环链表，通常使用尾指针来标识，可简化操作。

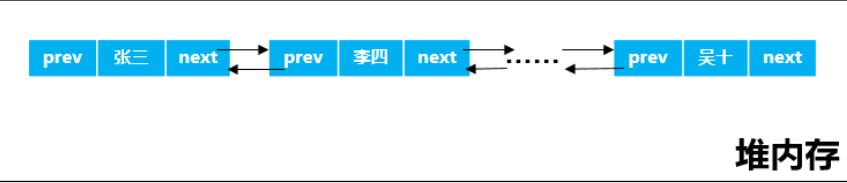
4、双向链表

双向链表即在单链表的基础上又添加了一个指针域，用来指向其前驱结点，使得在查找某个结点的前驱结点时不再需要从表头开始顺次查找，大大减小了事件复杂度，但相应的会增加内存的空间消耗。

 

 代码实现

package 双向链表;

/**
 * @author psy
 */
public class DBNode {
    int data;
    DBNode next;//下一个结点
    DBNode pre;//前一个结点
    public DBNode(int data) {
        this.data = data;
    }
}

package 双向链表;

/**
 * @author psy
 */
public class DBlinkList {
    //头节点
    DBNode head = new DBNode(0);

    //添加结点到双向链表（尾部添加）
    public void addDBNode(int data) {
        DBNode newNode = new DBNode(data);
        DBNode cur = head;//// 接收head头指针的对象
        while(cur.next != null)//遍历链表
            cur = cur.next;// 往后移动一个节点,指向下一个节点
            cur.next = newNode;//新增下一个结点
            newNode.pre = cur;//新结点的上一个结点是cur
    }

    //删除结点
    public void delete(int data) {
        if(head.next == null) {
            System.out.println("链表为空。");
            return;
        }
        DBNode cur = head.next;
        boolean flag = false;//标志是否找到待删除结点
        while(true) {
            if(cur == null){
                break;//已经遍历完这个链表
            }
           else if(cur.data == data) {//如果当前结点等于要删除的，就退出循环
                flag = true;
                break;
            }
            cur = cur.next;//后移
        }
        if(flag) {
            cur.pre.next = cur.next;//将上一个结点的后一个指针指向要删除节点的后续节点
            if(cur.next != null)//如果要删除节点的下一个节点不等于null
                cur.next.pre = cur.pre;//将下一个结点的前一个指针指向要删除结点的前一个结点....
        }else{

            System.out.printf("要删除的结点数据为%d不存在
",data);
        }
    }

    //显示结点
    public void print() {
        DBNode cur = head.next;
        while(cur !=null) {
            System.out.print(cur.data+" ");
            cur = cur.next;
        }
        System.out.println();
    }
}

package 双向链表;

/**
 * @author psy
 * 不仅可以指向下一个对象，还能指向上一个对象
 */
public class Temp {
    public static void main(String[] args) {
        DBlinkList mylist = new DBlinkList();
        mylist.addDBNode(1);
        mylist.addDBNode(2);
        mylist.addDBNode(3);
        mylist.addDBNode(4);

        System.out.println("双向链表：");
        mylist.print();

        System.out.println("删除后的双向链表：");
        mylist.delete(2);
        mylist.print();
    }
}

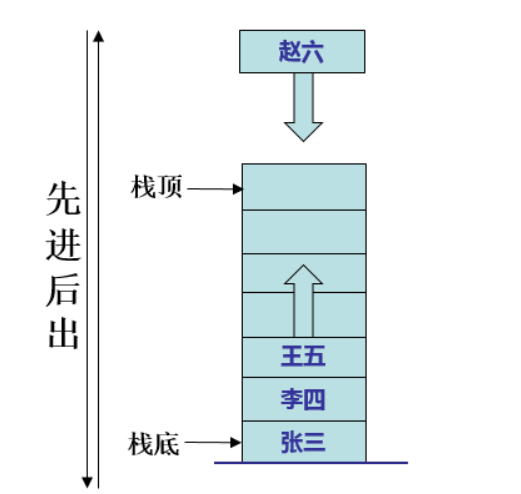
四、堆栈

栈是一种操作受限制的线性表。其限制是仅允许在线性表的尾部进行添加和删除操作，这一端被称为栈顶，另一端称为栈底。向一个栈添加新元素叫压栈，删除元素又称为出栈。

代码实现

用数组实现堆栈

package 堆栈;

/**
 * @author psy
 * 用数组实现堆栈
 */
public class ArrayOfStack {
    private Object[] stack = null;//初始数组
    private int size;//容量大小
    private int top;//top相当于数组下标

    //默认初始化一个栈堆,大小为100
    public ArrayOfStack(){
        this.size = 100;
        this.top = -1;//只是定义了没有赋值，所以等于-1
        this.stack = new Object[size];
    }

    //初始化一个自定义大小的栈堆
    public ArrayOfStack(int size){
        this.size = size;
        this.top = -1;
        this.stack = new Object[size];
    }

    /**
     * //判断堆栈是否为空
     * @return
     */
    public boolean isEmpty(){
        if(top == -1){
            return true;
        }else
            return false;
    }

//    /**
//     * 判断栈堆是否已满
//     * @return
//     */
//    public boolean isFull(){
//        if(top == (size-1)){
//            return true;
//        }else
//            return true;
//    }

    /**
     * 入栈操作
     * @param data
     */
    public void push(String data){

        //入栈开始，top相当于数组下标
        top++;
        stack[top] = data;
    }

    /**
     * 出栈
     * @return
     */
    public Object pop(){
        //定义一个临时对象
        Object val = null;
        //堆栈为空时报错
        if(isEmpty()){
            System.out.println("堆栈为空");
            return val;
        }
        //获取堆栈值
        val = stack[top];
        top--;
        return val;
    }

    /**
     * 获取栈顶元素
     * @return
     */
    public Object peek(){
        Object topVal = null;
        if(isEmpty()){
            System.out.println("栈堆为空!");
            return topVal;
        }
        //取出栈顶元素
        topVal = stack[top];
        return topVal;
    }

    /**
     * 获取堆栈元素,有几个元素
     * @return
     */
    public int size(){
        return top+1;
    }

    /**
     * 获取栈堆容量,可以存放多少个数据
     * @return
     */
    public int capcity(){
        return size;
    }
}

package 堆栈;

/**
 * @author psy
 */
public class Temp {
    public static void main(String[] args) {
        ArrayOfStack stack=new ArrayOfStack(10);
        stack.push("12");//入栈
        stack.push("2");
        stack.push("1");
        stack.pop();//出栈
        stack.pop();
        System.out.println(stack.peek());//获取栈顶，先进后出
        System.out.println(stack.size());//

    }
}

用链表实现堆栈

package 堆栈.链表堆栈;

/**
 * @author psy
 * 链表实现堆栈
 */
public class Node {
    //链表数据域
    Object data;
    //链域
    Node next;

    //构造头结点
    public Node(){
        this.data = null;
        this.next = null;
    }
    //构造节点
    public Node(Object data){
        this.data = data;
        this.next = null;
    }
}

package 堆栈.链表堆栈;

/**
 * @author psy
 */
public class LinkOfStack {
    //定义一个头结点
    private Node head;
    //构造头结点
    public LinkOfStack(){
        head = new Node();
    }

    //判断是否为空
    public boolean empty(){
        if(head.next == null)
            return true;
        else
            return false;
    }

    //堆栈入栈
    public void push(Object data){
        Node item = new Node(data);
        item.next = head.next;
        head.next = item;
    }

    //出栈
    public Object pop(){
        Object item = null;
        if(empty()){
            System.out.println("堆栈为空");
        }
        item = head.next.data;
        head.next = head.next.next;
        return item;
    }

    //堆栈大小
    public int size(){
        int len = 0;
        Node p = head;
        while(p.next != null){
            len++;
            p = p.next;
        }
        return len;
    }

    //获取栈顶元素
    public Object peek(){
        if(empty()){
            System.out.println("堆栈为空");
        }
        return head.next.data;
    }

    public static void main(String[] args){
        LinkOfStack stack = new LinkOfStack();
        stack.push("测试链表堆栈节点一");
        System.out.println(stack.size());
        System.out.println(stack.peek());
        while(!stack.empty()){
            System.out.print(stack.pop()+"-->");
        }
    }
}

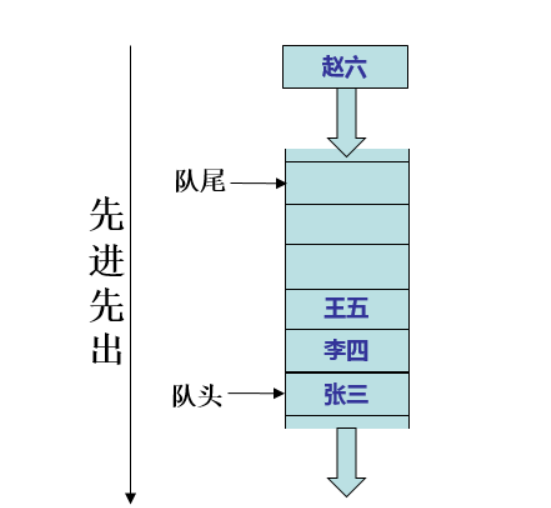
五、队列

队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队，从队列中删除一个队列元素称为出队。因为队列只允许在一端插入，在另一端删除，所以

只有最早进入队列的元素才能最先从队列中删除，故队列又称为先进先出（FIFO—first in first out）线性表。