顺序队列

顺序队列，即采用顺序表模拟实现的队列结构。

我们知道，队列具有以下两个特点：

1. 数据从队列的一端进，另一端出；
2. 数据的入队和出队遵循"先进先出"的原则；

因此，只要使用顺序表按以上两个要求操作数据，即可实现顺序队列。首先来学习一种最简单的实现方法。

顺序队列简单实现

由于顺序队列的底层使用的是数组，因此需预先申请一块足够大的内存空间初始化顺序队列。除此之外，为了满足顺序队列中数据从队尾进，队头出且先进先出的要求，我们还需要定义两个指针（top 和 rear）分别用于指向顺序队列中的队头元素和队尾元素，如图 1 所示：

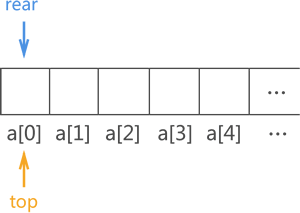
图 1 顺序队列实现示意图

由于顺序队列初始状态没有存储任何元素，因此 top 指针和 rear 指针重合，且由于顺序队列底层实现靠的是数组，因此 top 和 rear 实际上是两个变量，它的值分别是队头元素和队尾元素所在数组位置的下标。

在图 1 的基础上，当有数据元素进队列时，对应的实现操作是将其存储在指针 rear 指向的数组位置，然后 rear+1；当需要队头元素出队时，仅需做 top+1 操作。

例如，在图 1 基础上将 {1,2,3,4} 用顺序队列存储的实现操作如图 2 所示：

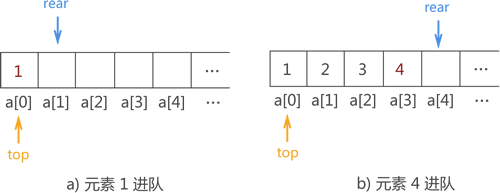
图 2 数据进顺序队列的过程实现示意图

在图 2 基础上，顺序队列中数据出队列的实现过程如图 3 所示：

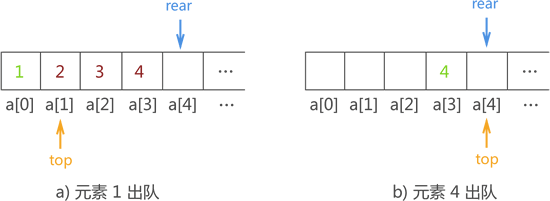
图 3 数据出顺序队列的过程示意图

因此，使用顺序表实现顺序队列最简单方法的 C 语言实现代码为：

1. #include <stdio.h>
2. int enQueue(int *a,int rear,int data){
3. a[rear]=data;
4. rear++;
5. return rear;
6. }
7. void deQueue(int *a,int front,int rear){
8. //如果 front==rear，表示队列为空
9. while (front!=rear) {
10. printf("出队元素：%d ",a[front]);
11. front++;
12. }
13. }
14. int main() {
15. int a[100];
16. int front,rear;
17. //设置队头指针和队尾指针，当队列中没有元素时，队头和队尾指向同一块地址
18. front=rear=0;
19. //入队
20. rear=enQueue(a, rear, 1);
21. rear=enQueue(a, rear, 2);
22. rear=enQueue(a, rear, 3);
23. rear=enQueue(a, rear, 4);
24. //出队
25. deQueue(a, front, rear);
26. return 0;
27. }

程序输出结果：

出队元素：1
出队元素：2
出队元素：3
出队元素：4

此方法存在的问题

先来分析以下图 2b) 和图 3b)。图 2b) 是所有数据进队成功的示意图，而图 3b) 是所有数据全部出队后的示意图。通过对比两张图，你会发现，指针 top 和 rear 重合位置指向了  a[4] 而不再是 a[0]。也就是说，整个顺序队列在数据不断地进队出队过程中，在顺序表中的位置不断后移。

顺序队列整体后移造成的影响是：

• 顺序队列之前的数组存储空间将无法再被使用，造成了空间浪费；
• 如果顺序表申请的空间不足够大，则直接造成程序中数组 a 溢出，产生溢出错误；

为了避免以上两点，我建议初学者使用下面的方法实现顺序队列。

顺序队列另一种实现方法

既然明白了上面这种方法的弊端，那么我们可以试着在它的基础上对其改良。

为了解决以上两个问题，可以使用巧妙的方法将顺序表打造成一个环状表，如图 4 所示：

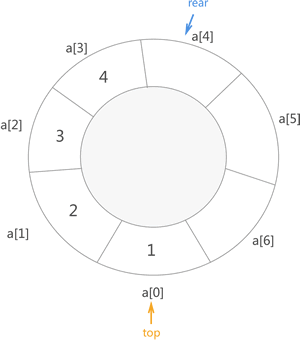
图 4 环状顺序队列

图 4 只是一个想象图，在真正的实现时，没必要真创建这样一种结构，我们还是使用之前的顺序表，也还是使用之前的程序，只需要对其进行一点小小的改变：

1. #include <stdio.h>
2. #define max 5//表示顺序表申请的空间大小
3. int enQueue(int *a,int front,int rear,int data){
4. //添加判断语句，如果rear超过max，则直接将其从a[0]重新开始存储，如果rear+1和front重合，则表示数组已满
5. if ((rear+1)%max==front) {
6. printf("空间已满");
7. return rear;
8. }
9. a[rear%max]=data;
10. rear++;
11. return rear;
12. }
13. int deQueue(int *a,int front,int rear){
14. //如果front==rear，表示队列为空
15. if(front==rear%max) {
16. printf("队列为空");
17. return front;
18. }
19. printf("%d ",a[front]);
20. //front不再直接 +1，而是+1后同max进行比较，如果=max，则直接跳转到 a[0]
21. front=(front+1)%max;
22. return front;
23. }
24. int main() {
25. int a[max];
26. int front,rear;
27. //设置队头指针和队尾指针，当队列中没有元素时，队头和队尾指向同一块地址
28. front=rear=0;
29. //入队
30. rear=enQueue(a,front,rear, 1);
31. rear=enQueue(a,front,rear, 2);
32. rear=enQueue(a,front,rear, 3);
33. rear=enQueue(a,front,rear, 4);
34. //出队
35. front=deQueue(a, front, rear);
36. //再入队
37. rear=enQueue(a,front,rear, 5);
38. //再出队
39. front=deQueue(a, front, rear);
40. //再入队
41. rear=enQueue(a,front,rear, 6);
42. //再出队
43. front=deQueue(a, front, rear);
44. front=deQueue(a, front, rear);
45. front=deQueue(a, front, rear);
46. front=deQueue(a, front, rear);
47. return 0;
48. }

程序运行结果：

1 2 3 4 5 6

使用此方法需要注意的是，顺序队列在判断数组是否已满时，出现下面情况：

• 当队列为空时，队列的头指针等于队列的尾指针；
• 当数组满员时，队列的头指针等于队列的尾指针；

顺序队列的存储状态不同，但是判断条件相同。为了对其进行区分，最简单的解决办法是：牺牲掉数组中的一个存储空间，判断数组满员的条件是：尾指针的下一个位置和头指针相遇，就说明数组满了，即程序中第 5 行所示。