首先,了解几个相关概念。
频数:在一组样本数据中,不同的数据出现的次数有多有少,或者说它们出现的频繁程度不同,我们称每个数据出现的次数为频数。
频率:每个数据出现的次数与样本数据总量的比值为频率。
组数:把全体样本数据分成的组的个数(当数据总量在100个以内时,常常分为5~12组)。
组距:把全体样本数据分成若干个组,每个小组在x轴上的两个左右端点的距离。
极差:全体样本数据中的最大值与最小值的差。
由以上定义,可以得到下面的关系:
频数 极差
频率 = ———————— , 组距 = ———————
样本总数 组数
频率分布直方图(Frequency distribution histogram):
在直角坐标系中,横轴表示样本数据的连续可取数值,按数据的最小值和最大值把样本数据分为m组,使最大值和最小值落在开区间(a,b)内,a略小于样本数据的最小值,b略大于样本数据的最大值。组距为d=(b-a)/m,各数据组的边界范围按左闭右开区间,如[a,a+d),[a+d,a+2d),……[a+(m-1)d,b)。纵轴表示频率除以组距(落在各组样本数据的个数称为频数,频数除以样本总数为频率)的值,以频率和组距的商为高、组距为底的矩形在直角坐标系上来表示,由此画成的统计图叫做频率分布直方图。
频数分布直方图:
通过长方形的高代表对应组的频数与组距的比(因为组距是一个常数,为了画图和看图方便,通常直接用高表示频数),这样的统计图称为频数分布直方图。频数分布直方图能:①清楚显示各组频数分布情况;②易于显示各组之间频数的差别。
由以上两个定义可知,频率分布直方图和频数分布直方图的关系如下:
① 二者的横坐标是一样的,都是代表样本数据,且组距相同;
② 二者的直方图的高度变化是一样的;
③ 二者的纵坐标是不一样的,前者为频率和组距的比值;后者为频数。
如下所示:
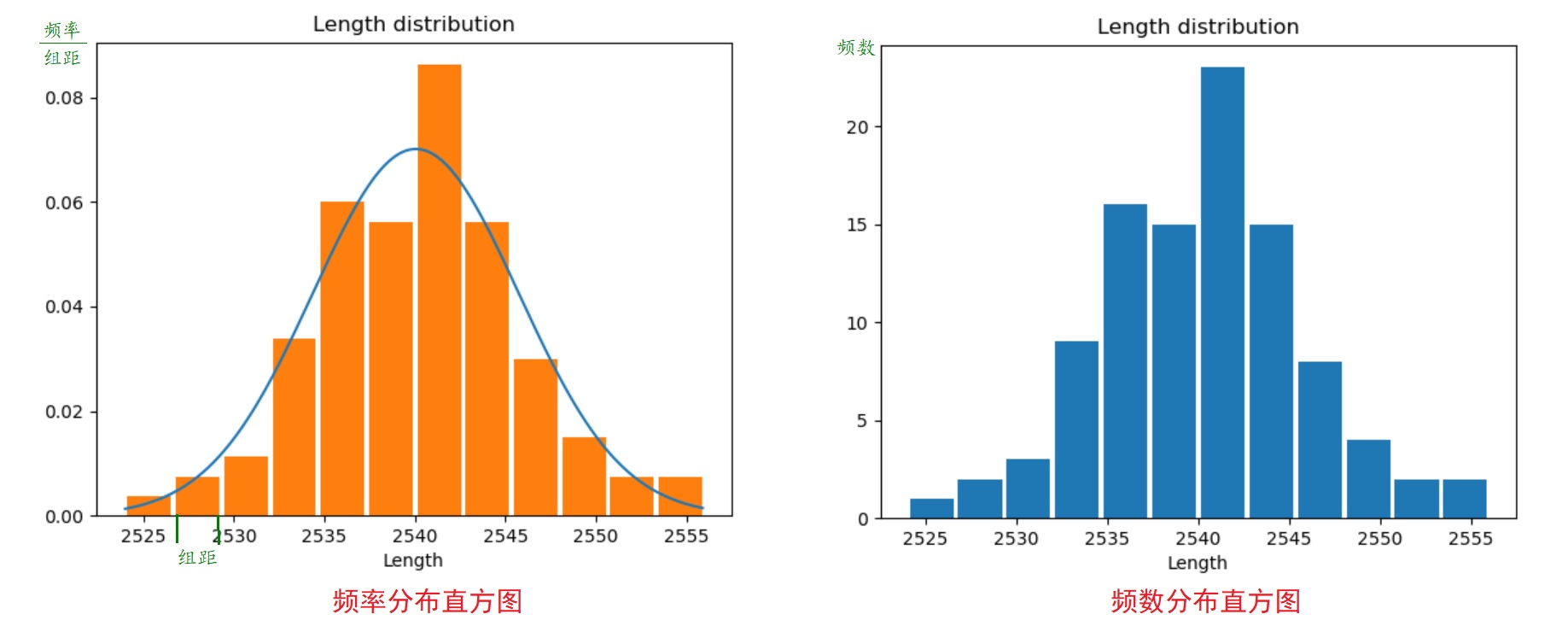
在频率分布直方图中,同时也绘制了正态分布曲线。那么,如何在频数分布直方图上绘制一条类似正态分布曲线的曲线呢?
答案是:只要把频率分布直方图中的正态分布曲线进行一定比例的放大即可。那么,这个比例到底是多少呢?下面来计算一下。
频率 频数 / 样本总数 组数 组数 ———— = —————————————— = 频数 × ————————————————— = 频数 × ———————————————————————————————————————— 组距 极差 / 组数 样本总数 × 极差 样本总数 ×(样本中的最大值 - 样本中的最小值)
还需要注意的一点是绘图时纵坐标表示的单位高度,一般是等于多少像素。可以表示为:
纵坐标的总体高度
单位高度 = ————————————————
纵坐标的表示范围
假设f(x)正态分布曲线的概率密度函数,那么在频数分布直方图上绘制正态分布曲线时,曲线的瞬时值大小为:
样本总数 × (样本中的最大值 - 样本中的最小值) 纵坐标的总体高度
———————————————————————————————————————————— × ———————————————— × 概率密度函数
组数 纵坐标的表示范围