上一篇:https://www.cnblogs.com/pylblog/p/8370980.html
| 类型 | 属性1 | 属性2 | 属性3 | 属性4 |
| A | 3 | 2 | 1 | 1 |
| A | 1 | 2 | 1 | 2 |
| A | 1 | 2 | 3 | 3 |
| B | 2 | 2 | 1 | 1 |
| B | 2 | 2 | 2 | 1 |
| B | 2 | 1 | 2 | 2 |
| B | 1 | 1 | 3 | 2 |
| B | 1 | 1 | 3 | 3 |
上面每个属性,都是枚举的
上面每个属性,有可以按下面的树来表达:



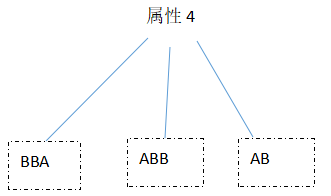
假如有一个最好的分类方法,那一定是立即根据不同的值,将AB分成两组。
所以,对于哪一个属性分类的能力高低,可以用有多少个样本,位于同质子集中衡量。
如:
属性1得分为 3 + 1 = 4
属性2得分为3
属性3得分为2
属性4得分为0
从而,可以构建树:

但是,如果按上面这样,一次就想试图将树建出来,去到后面得分太低的属性,或者得分相同的属性,就很难建立出来了。
所以,在得出属性1的分发的时候,要去除值2,值3的同质集合,从新构筑树:
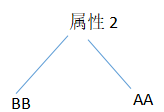


然后,减去分析属性2的样本,已经没有样本了
所以,最终, 这树:

甚至,可以发现,用属性2就可以解决这个分类问题了。
对属性分类能力的高低,还可以使用无序度(熵)来衡量。
假如有二值,期样本量分别为P和N,T = P + N
那么,无序度D = - P / T * log2 P/T - N/T * log2N/T

由图可以看出,P样本占据总样本的数量越多,或越小,熵越少;
那么,对于每个属性,其分类能力 Q = Σ D,即每个分支的无序度之和,越小越好;
但是,有一个问题,各个分支的权重是一样的,也就是说,如果样本不足,导致某个属性枚举值分支没有样本,那无序度岂不是为0(最好了),这显然不是最合理的。
所以:
Q = Σ ( D * 分支样本数 / 总样本数)
对于属性1:

Q1 = 1/2
同理,对于其他属性
Q2≈0.6
Q3≈0.7
Q4≈0.95
然后,可以去除属性1中,值2和值3的样本,剩余的样本继续再一轮计算属性2,属性3,属性4的熵,得出第二个分支。