本文介绍如何利用决策树/判定树(decision tree)中决策树归纳算法(ID3)解决机器学习中的回归问题。文中介绍基于有监督的学习方式,如何利用年龄、收入、身份、收入、信用等级等特征值来判定用户是否购买电脑的行为,最后利用python和sklearn库实现了该应用。
1、 决策树归纳算法(ID3)实例介绍
2、 如何利用python实现决策树归纳算法(ID3)
1、决策树归纳算法(ID3)实例介绍
首先介绍下算法基本概念,判定树是一个类似于流程图的树结构:其中,每个内部结点表示在一个属性上的测试,每个分支代表一个属性输出,而每个树叶结点代表类或类分布。树的最顶层是根结点。
决策树的优点: 直观,便于理解,小规模数据集有效
决策树的缺点:处理连续变量不好,类别较多时,错误增加的比较快,可规模性一般
以如下测试数据为例:
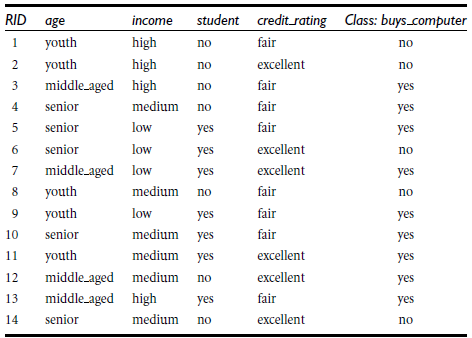
我们有一组已知训练集数据,显示用户购买电脑行为与各个特征值的关系,我们可以绘制出如下决策树图像(绘制方法后面介绍)
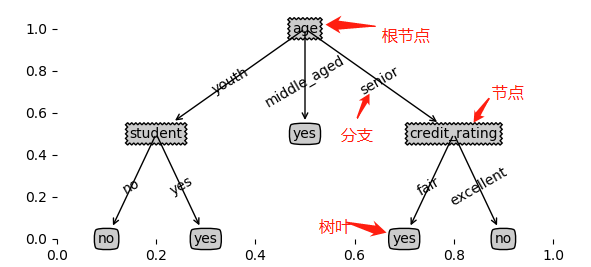
此时,输入一个新的测试数据,就能根据该决策树很容易判定出用户是否购买电脑的行为。
有两个关键点需要考虑:1、如何决定分支终止;2如何决定各个节点的位置,例如根节点如何确定。
1、如何决定分支终止
如果某个节点所有标签均为同一类,我们将不再继续绘制分支,直接标记结果。或者分支过深,可以基于少数服从多数的算法,终止该分支直接绘制结果。
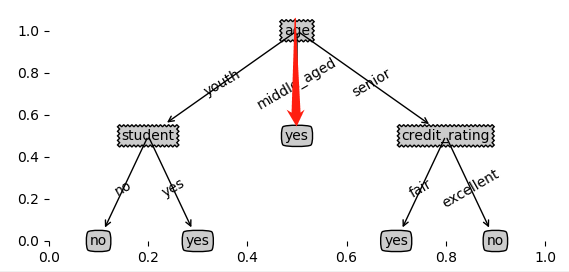
例如,通过年龄划分,所有middle_aged对象,对应的标签都为yes,尽管还有其它特征值,例如收入、身份、信用等级等,但由于标签所有都为一类,所以该分支直接标注结果为yes,不再往下细分。
2、如何决定各个节点的位置,例如根节点如何确定。
在说明这个问题之前,我们先讨论一个熵的概,信息和抽象,如何度量?1948年,香农提出了 “信息熵(entropy)”的概念,一条信息的信息量大小和它的不确定性有直接的关系,要搞清楚一件非常非常不确定的事情,或者是我们一无所知的事情,需要了解大量信息==>信息量的度量就等于不确定性的多少
例子:猜世界杯冠军,假如一无所知,猜多少次?每个队夺冠的几率不是相等的,也就说明该信息熵较大。
当前样本集合 D 中第 k 类样本所占的比例为 pk ,则 D 的信息熵定义为
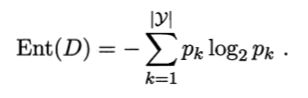
离散属性 a 有 V 个可能的取值 {a1,a2,…,aV};样本集合中,属性 a 上取值为 av 的样本集合,记为 Dv。用属性 a 对样本集 D 进行划分所获得的“信息增益”,表示得知属性 a 的信息而使得样本集合不确定度减少的程,公式如下:
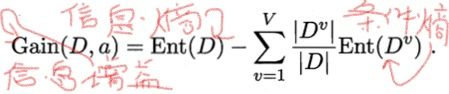
ID3算法首先计算各个特征向量的信息增益量,取最大的作为决策树的根,利用上面公式,以计算age年龄的信息增益量为例:

于是,我们选取age年龄作为决策树的根节点,依次画出最后的决策树,最后的算法如下:
-
- 树以代表训练样本的单个结点开始(步骤1)。
- 如果样本都在同一个类,则该结点成为树叶,并用该类标号(步骤2 和3)。
- 否则,算法使用称为信息增益的基于熵的度量作为启发信息,选择能够最好地将样本分类的属性(步骤6)。该属性成为该结点的“测试”或“判定”属性(步骤7)。在算法的该版本中,
- 所有的属性都是分类的,即离散值。连续属性必须离散化。
- 对测试属性的每个已知的值,创建一个分枝,并据此划分样本(步骤8-10)。
- 算法使用同样的过程,递归地形成每个划分上的样本判定树。一旦一个属性出现在一个结点上,就不必该结点的任何后代上考虑它(步骤13)。
- 递归划分步骤仅当下列条件之一成立停止:
- (a) 给定结点的所有样本属于同一类(步骤2 和3)。
- (b) 没有剩余属性可以用来进一步划分样本(步骤4)。在此情况下,使用多数表决(步骤5)。
- 这涉及将给定的结点转换成树叶,并用样本中的多数所在的类标记它。替换地,可以存放结
- 点样本的类分布。
- (c) 分枝
- test_attribute = a i 没有样本(步骤11)。在这种情况下,以 samples 中的多数类
- 创建一个树叶(步骤12)
除了ID3算法,还有一些其它算法可以用来绘制决策树,此处暂不讨论,例如:C4.5: Quinlan,Classification and Regression Trees (CART): (L. Breiman, J. Friedman, R. Olshen, C. Stone)。共同点:都是贪心算法,自上而下(Top-down approach)。区别:属性选择度量方法不同: C4.5 (gain ratio), CART(gini index), ID3 (Information Gain)
2、 如何利用python实现决策树归纳算法(ID3)
用Python实现上面实例前,我们需要先安装一个科学库Anaconda,anaconda指的是一个开源的Python发行版本,其包含了conda、Python等180多个科学包及其依赖项。
同时,还需要安装一个决策树图形绘制工具graphviz
下面是具体的代码实现
# 导入库 from sklearn.feature_extraction import DictVectorizer import csv from sklearn import tree from sklearn import preprocessing from sklearn.externals.six import StringIO import math # 测试,没有age时的信息熵 result = -(5/14*math.log2(5/14) + 9/14*math.log2(9/14)) print(result) #测试,有age时的信息熵 result1 = 5/14*(-3/5*math.log2(3/5) - 2/5*math.log(2/5)) + 4/14*(-4/4*math.log2(4/4)) + 5/14*(-3/5*math.log2(3/5) - 2/5*math.log2(2/5)) print(result1) # 1 打开测试数据集 allElectronicsData = open(r'D: est.csv','r') reader = csv.reader(allElectronicsData) # 读取文件头 headers = next(reader) #print(headers) featureList = [] labelList = [] # 2 为每个测试样例,建立一个特征名和值的字典,然后加入到featureList中 for row in reader: labelList.append(row[len(row) -1]) rowDict = {} for i in range(1,len(row) -1): rowDict[headers[i]] = row[i] featureList.append(rowDict) print(labelList) print(featureList) # 3 把输入特征集进行转换,例如 ''' {'age': 'youth', 'income': 'high', 'student': 'no', 'credit_rating': 'fair'} [ 0. 0. 1. 0. 1. 1. 0. 0. 1. 0.] ''' vec = DictVectorizer() dummyX = vec.fit_transform(featureList).toarray() #print(type(dummyX)) print(dummyX) #print(vec.get_feature_names()) # 4 对标签值进行0,1转换 lb = preprocessing.LabelBinarizer() dummyY = lb.fit_transform(labelList) print(dummyY) # 5 直接调用库的决策树分类器,entropy表示信息熵 clf = tree.DecisionTreeClassifier(criterion='entropy') clf = clf.fit(dummyX,dummyY) #print(clf) # 6 填入feature_names,还原原有的值,写入test.dot文件 with open("test.dot",'w') as f: f = tree.export_graphviz(clf,feature_names=vec.get_feature_names(),out_file=f) # 7 此时dumyX为一个n维的向量,取出第一行,修改一下作为一个新的测试数据 # 'age': 'middle_aged', 'income': 'high', 'student': 'no', 'credit_rating': 'fair' 正确结果应该是 买 为1 oneRowX = dummyX[0,:] print("oneRowX: ",oneRowX) newRowX = oneRowX newRowX[0] = 1 newRowX[2] = 0 print(newRowX) # 8 使用新数据进行测试验证 predictedY = clf.predict(newRowX.reshape(1, -1)) print(predictedY) # 使用graphviz工具,通过命令dot -Tpdf test.dot -o output.pdf生成决策树文档