python数据分析算法（决策树2）CART算法

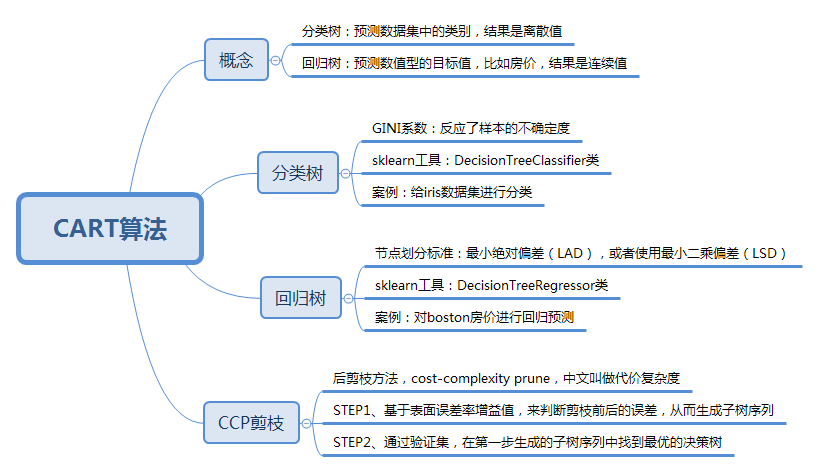
CART（Classification And Regression Tree）,分类回归树，，决策树可以分为ID3算法，C4.5算法，和CART算法。ID3算法，C4.5算法可以生成二叉树或者多叉树，CART只支持二叉树，既可支持分类树，又可以作为回归树。

分类树： 基于数据判断某物或者某人的某种属性（个人理解）可以处理离散数据，就是有限的数据，输出样本的类别

回归树： 给定了数据，预测具体事物的某个值；可以对连续型的数据进行预测，也就是数据在某个区间内都有取值的可能，它输出的是一个数值

CART 分类树的工作流程

CART和C4.5算法类似，知识属性选择的指标采用的是基尼系数，基尼系数本身反应了样本的不确定度，当基尼系数越小的时候，说明样本之间的差异性小，不确定度低。分类的过程是一个不确定度降低的过程，即纯度提升的过程，所以构造分类树的时候会基于基尼系数最小的属性作为划分。

了解基尼系数：

假设t为节点，那么该节点的GINI系数的计算公式为：

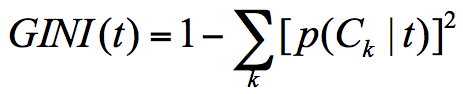
p(Ck|t) 表示t属性类别Ck的概率，节点t的基尼系数为1减去各个分类Ck概率平方和    

例如集合1： 6个人去游泳，  那么p(Ck|t)=1，因此  GINI（t） = 1-1 =0

集合2      ：  3个人去游泳，3个人不去，那么p(C1k|t) = 0.5 ，p(C2k|t) = 0.5    

得出，集合1样本基尼系数最小，样本最稳定，2的样本不稳定性大

该公式表示节点D的基尼系数等于子节点D1,D2的归一化基尼系数之和

使用CART算法创建分类树

iris是sklearn 自带IRIS（鸢尾花）数据集sklearn中的来对特征处理功能进行说明包含4个特征（Sepal.Length（花萼长度）、Sepal.Width（花萼宽度）、Petal.Length（花瓣长度）、Petal.Width（花瓣宽度）），特征值都为正浮点数，单位为厘米

目标值为鸢尾花的分类（Iris Setosa（山鸢尾）、Iris Versicolour（杂色鸢尾），Iris Virginica（维吉尼亚鸢尾））

 1 # encoding=utf-8
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
# 准备数据集
iris=load_iris()
# 获取特征集和分类标识
features = iris.data
labels = iris.target
# 随机抽取 33% 的数据作为测试集，其余为训练集 使用sklearn.model_selection train_test_split 训练
train_features, test_features, train_labels, test_labels = train_test_split(features, labels, test_size=0.33, random_state=0)
# 创建 CART 分类树
clf = DecisionTreeClassifier(criterion='gini')
# 拟合构造 CART 分类树
clf = clf.fit(train_features, train_labels)
# 用 CART 分类树做预测  得到预测结果
test_predict = clf.predict(test_features)
# 预测结果与测试集结果作比对
score = accuracy_score(test_labels, test_predict)
print("CART 分类树准确率 %.4lf" % score)

 CART 分类树准确率 0.9600

train_test_split 可以把数据集抽取一部分作为测试集，就可以德奥训练集和测试集

14 初始化一棵cart树，16 训练集的特征值和分类表示作为参数进行拟合得到cart分类树

cart回归树的工作流程

cart回归树划分数据集的过程和分类树的过程是一样的，回归树得到的预测结果是连续值，评判不纯度的指标不同，分类树采用的是基尼系数，回归树需要根据样本的离散程度来评价 不纯度

样本离散程度计算方式，每个样本值到均值的差值，可以去差值的绝对值，或者方差

         方差为每个样本值减去样本均值的平方和除以样本可数

最小绝对偏差（LAD） 最小二乘偏差

 如何使用CART回归树做预测

这里使用sklearn字典的博士度房价数据集，该数据集给出了影响房价的一些指标，比如犯罪了房产税等，最后给出了房价

# encoding=utf-8
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
from sklearn.tree import DecisionTreeRegressor
# 准备数据集
boston=load_boston()
# 探索数据
print(boston.feature_names)
# 获取特征集和房价
features = boston.data
prices = boston.target
# 随机抽取 33% 的数据作为测试集，其余为训练集
train_features, test_features, train_price, test_price = train_test_split(features, prices, test_size=0.33)
# 创建 CART 回归树
dtr=DecisionTreeRegressor()
# 拟合构造 CART 回归树
dtr.fit(train_features, train_price)
# 预测测试集中的房价
predict_price = dtr.predict(test_features)
# 测试集的结果评价
print('回归树二乘偏差均值:', mean_squared_error(test_price, predict_price))
print('回归树绝对值偏差均值:', mean_absolute_error(test_price, predict_price)) 

['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
 'B' 'LSTAT']
回归树二乘偏差均值： 32.065568862275455
回归树绝对值偏差均值 3.2892215568862277

cart决策树的剪枝 

cart决策树剪枝采用的是CCP方法，一种后剪枝的方法，cost-complexity prune 中文：代价复杂度，这种剪枝用到一个指标 叫做  节点的表面误差率增益值，以此作为剪枝前后误差的定义

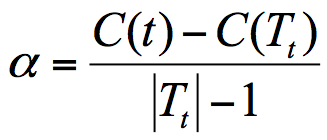 Tt 代表以t为根节点的子树，C（Tt）表示节点t的子树没被裁剪时子树Tt的误差，C(t)表示节点t的子树被剪枝后节点t的误差，|Tt|代子树Tt的叶子树，剪枝后，T的叶子树减一

所以节点的表面误差率增益值 等于 节点t的子树被剪枝后的误差变化除以 减掉的叶子数量

因此希望剪枝前后误差最小，所以我们要寻找就是最小α值对应的节点，把它减掉。生成第一个子树，重复上面过程继续剪枝，知直到最后为根节点，即为最后一个子树

得到剪枝后的子树集合后，我们需要采用验证集对所有子树的误差计算一遍，可以计算每个子树的基尼指数或平房误差，去最小的那棵树