铺设道路road.cpp时空限制1000ms / 128MB(贪心)
题目描述
春春是一名道路工程师,负责铺设一条长度为 n 的道路。
铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 n 块首尾相连的区域,一开始,第 ii 块区域下陷的深度为di 。
春春每天可以选择一段连续区间[L,R] ,填充这段区间中的每块区域,让其下陷深度减少 1。在选择区间时,需要保证,区间内的每块区域在填充前下陷深度均不为 0 。
春春希望你能帮他设计一种方案,可以在最短的时间内将整段道路的下陷深度都变为 0 。
输入输出格式
输入格式:road.in
输入文件包含两行,第一行包含一个整数 n,表示道路的长度。 第二行包含 n 个整数,相邻两数间用一个空格隔开,第i 个整数为 di 。
输出格式:road.out
输出文件仅包含一个整数,即最少需要多少天才能完成任务。
输入输出样例
输入样例:
6
4 3 2 5 3 5
输出样例#1:
9
说明
【样例解释】
一种可行的最佳方案是,依次选择: [1,6]、[1,6]、[1,2]、[1,1]、[4,6]、[4,4]、[4,4]、[6,6]、[6,6]。
【数据规模与约定】
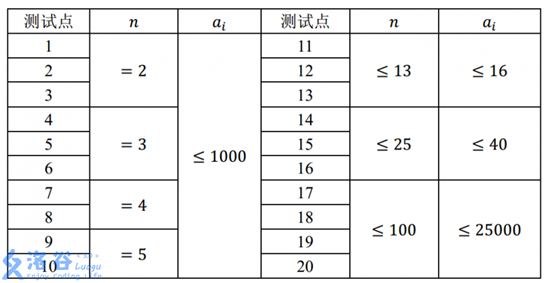
对于 30% 的数据,1≤n≤10 ;
对于 70% 的数据,1≤n≤1000 ;
对于 100% 的数据,1≤n≤100000,0≤di≤10000 。
【思路】:
首先要考虑一个问题,填深坑时会把浅的也一起填起来,所以只要用深的减去浅的,求和就是答案
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> #include<stack> #include<vector> #include<map> #include<string> #include<cstring> using namespace std; const int maxn=999999999; const int minn=-999999999; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int n,a[1000080]; int main() { cin>>n; for(int i=1;i<=n;++i) { a[i]=read(); } int ans=a[1]; for(int i=2;i<=n;++i) { if(a[i]>a[i-1]) ans+=(a[i]-a[i-1]); } cout<<ans; return 0; }
2、货币系统(money.cpp)时空限制1000ms / 128MB
题目描述
在网友的国度中共有 n 种不同面额的货币,第 i 种货币的面额为 a[i],你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为 n、面额数组为 a[1..n] 的货币系统记作 (n,a)。
在一个完善的货币系统中,每一个非负整数的金额 x 都应该可以被表示出,即对每一个非负整数 x,都存在 n 个非负整数 t[i] 满足 a[i]×t[i] 的和为 x。然而, 在网友的国度中,货币系统可能是不完善的,即可能存在金额 x不能被该货币系统表示出。例如在货币系统 n=3, a=[2,5,9] 中,金额 1,3 就无法被表示出来。
两个货币系统 (n,a) 和 (m,b) 是等价的,当且仅当对于任意非负整数 x,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。他们希望找到一个货币系统 (m,b),满足 (m,b) 与原来的货币系统 (n,a)等价,且 m 尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的 m。()
输入格式:money.in
输入文件的第一行包含一个整数 T,表示数据的组数。
接下来按照如下格式分别给出 T 组数据。 每组数据的第一行包含一个正整数 n。接下来一行包含 n 个由空格隔开的正整数 a[i]。
输出格式:money.out
输出文件共有 T 行,对于每组数据,输出一行一个正整数,表示所有与 (n,a) 等价的货币系统 (m,b) 中,最小的 m。
输入输出样例
输入样例#1:
2
4
3 19 10 6
5
11 29 13 19 17
输出样例#1:
2
5
说明
在第一组数据中,货币系统 (2, [3,10]) 和给出的货币系统 (n, a) 等价,并可以验证不存在 m < 2的等价的货币系统,因此答案为 2。 在第二组数据中,可以验证不存在 m < n的等价的货币系统,因此答案为 5。
【数据范围与约定】
【思路】:
其实这破题我一开始就没读懂(雾?)后来研究了一下样例发现6不合法的原因是因为6=3+3=3*3,而19=10+6+3所以把它们删去
样例2中没有任意一个数会被其他的数的积或者和表示所以答案是5(嘿嘿)
解法一:
求完全背包完全背包的方案数,可以把要表示的大面额看成背包容量,把小面额看成单个物品的重量就成了完全背包。
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> #include<stack> #include<vector> #include<map> #include<string> #include<cstring> using namespace std; const int maxn=999999999; const int minn=-999999999; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); } while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } /*完全背包*/ const int N=255555; int all_beibao[N],f[N],n,by,js; void start() { memset(f,0,sizeof(f)); memset(all_beibao,0,sizeof(all_beibao)); js=0 ; } int main () { scanf("%d",&by); while(by--) { start(); n=read(); for(int i=1; i<=n; ++i) { f[i]=read(); } sort(f+1,f+1+n); all_beibao[0]=1 ; for(int i=1; i<=n; ++i) { if(!all_beibao[f[i]]) { js++; } for(int j=f[i]; j<=f[n]; ++j) { all_beibao[j]+=all_beibao[j-f[i]]; } } printf("%d ",js); } return 0 ; }
解法二:
竟然小数可以表示出大数,我们的目的是要把大数先删掉那就可以从小到大排序后把小数能表示的数求出来然后删掉(其实这才是我真正的思路,只不过比较傻)
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> #include<stack> #include<vector> #include<map> #include<string> #include<cstring> using namespace std; const int maxn=999999999; const int minn=-999999999; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); } while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int n,t,a[25555],visit[25555],ans; int main() { cin>>t; while(t--) { ans=0; cin>>n; memset(visit,0,sizeof(visit)); for(int i=1; i<=n; ++i) { cin>>a[i]; } sort(a+1,a+1+n); for(int i=1; i<=n; ++i) { if(!visit[a[i]]) ans++; for(int j=1; j<=a[n]; ++j) { if(j*a[i]<=a[n]) { visit[j*a[i]]=1; } else break; } //判断从a[i]到a[n]的每个数是否可以表示 for(int j=a[i]; j<=a[n]; ++j) { if(visit[j-a[i]]) visit[j]=1; } } cout<<ans<<' '; } return 0; }
、寻找道路find.cpp时空限制1000ms / 128MB
题目描述
在有向图 G 中,每条边的长度均为 1,现给定起点和终点,请你在图中找一条从起点到终点的路径,该路径满足以下条件:
路径上的所有点的出边所指向的点都直接或间接与终点连通。
在满足条件1的情况下使路径最短。
注意:图 G 中可能存在重边和自环,题目保证终点没有出边。
请你输出符合条件的路径的长度。
输入格式:road.in
第一行有两个用一个空格隔开的整数 n 和 m,表示图有 n 个点和 m 条边。
接下来的 m 行每行 2 个整数 x,y,之间用一个空格隔开,表示有一条边从点 x 指向点y。
最后一行有两个用一个空格隔开的整数 s, t,表示起点为 s,终点为 t。
输出格式:road.out
输出只有一行,包含一个整数,表示满足题目描述的最短路径的长度。如果这样的路径不存在,输出-1。
输入输出样例
输入样例#1:
3 2
1 2
2 1
1 3
输出样例#1:
-1
输入样例#2:
6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5
输出样例#2:
3
说明
解释1:
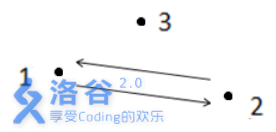
如上图所示,箭头表示有向道路,圆点表示城市。起点1与终点3不连通,所以满足题目描述的路径不存在,故输出-1 。
解释2:
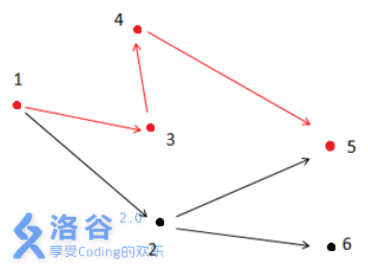
如上图所示,满足条件的路径为1- >3- >4- >5。注意点2 不能在答案路径中,因为点2连了一条边到点6 ,而点6不与终点5 连通。
【数据范围】
对于30%的数据,0<n≤10,0<m≤20;
对于60%的数据,0<n≤100,0<m≤2000;
对于100%的数据,0<n≤10000,0<m≤200000,0<x,y,s,t≤n,x,s≠t。
【思路】:反向建图从终点向起点用bfs删除掉相连的点,然后跑spfa
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> #include<stack> #include<vector> #include<map> #include<string> #include<cstring> using namespace std; const int maxn=0x3f3f3f; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); } while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } struct node { int to,next; } edge[300006]; int n,m,bx,by,x,y,dis[300006],head[300006],visit[300006],flag[300006],sum; void add(int u,int v) { edge[++sum].next=head[u]; edge[sum].to=v; head[u]=sum; } void spfa(int w) { queue<int>q; memset(visit,0,sizeof(visit)); memset(dis,maxn,sizeof(dis)); q.push(w); dis[w]=0; visit[w]=1; while(!q.empty()) { int u=q.front(); q.pop(); visit[u]=0; for(int i=head[u]; i; i=edge[i].next) { int v=edge[i].to; int z=1; if(dis[v]>dis[u]+z&&flag[v]) { dis[v]=dis[u]+1; if(!visit[v]) { visit[v]=1; q.push(v); } } } } } void bfs(int by) { queue<int>q; memset(visit,0,sizeof(visit)); q.push(by); flag[by]=visit[by]=1; while(!q.empty()) { int u=q.front(); q.pop(); for(int i=head[u]; i; i=edge[i].next) if(!visit[edge[i].to]) { visit[edge[i].to]=1; flag[edge[i].to]=1; q.push(edge[i].to); } } } void begin_read() { n=read(); m=read(); for(int i=1; i<=m; i++) { x=read(); y=read(); add(y,x); } bx=read(); by=read(); } void delete_edge() { for(int i=1; i<=n; i++) { if(!visit[i]) { for(int j=head[i]; j; j=edge[j].next) { int u=edge[j].to; if(flag[u]) flag[u]=0; } } } } int main() { begin_read(); bfs(by); for(int i=1; i<=n; i++) { visit[i]=flag[i]; } delete_edge(); spfa(by); if(dis[bx]<=maxn) printf("%d",dis[bx]); else printf("-1"); return 0; }