P1006 传纸条

题目链接：

P1006 传纸条

思路

第一种((O(n^2 cdot m^2))):

设$ f[i][j][k][l] (为从小渊传到小轩的纸条到达)(i,j) (，从小轩传给小渊的纸条到达)(k,l)$的路径上取得的最大的好心程度和。

从给定的起点出发走到指定位置的两条最短严格不相交路线。

那么特别显然，转移方程是

[f[i][j][k][l]=max( f[i][j-1][k-1][l] , f[i-1][j][k][l-1] , f[i][j-1][k][l-1] , f[i-1][j][k-1][l] )+a[i][j]+a[k][l] ]

注意(j)要从(i+1)开始循环，因为要避免走重复的路，有空画个图解释一下

60分代码

错误原因:

(m,n)很混乱

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<string>
#include<cstring>
using namespace std;
inline int read() {
    char c = getchar();
    int x = 0, f = 1;
    while(c < '0' || c > '9') {
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}
int  f[51][51][51][51],m,n;
int a[51][51];
signed main() {
    cin>>m>>n;
    for(int i=1; i<=n; ++i)
        for(int j=1; j<=m; ++j)
            cin>>a[i][j];
    for(int i=1; i<=m; ++i) {
        for(int j=1; j<=n; ++j) {
            for(int k=1; k<=m; ++k) {
                for(int p=j+1; p<=n; ++p) {
                    f[i][j][k][p]=max(max(f[i][j-1][k-1][p],f[i-1][j][k][p-1] ),max(f[i][j-1][k][p-1],f[i-1][j][k-1][p]) )+a[i][j]+a[k][p];
                }
            }
        }
    }
    //cout<<f[1][1][m][n];
    cout<<f[n][m-1][n-1][m];
    return 0;
}

100分代码:

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<string>
#include<cstring>
using namespace std;
inline int read() {
	char c = getchar();
	int x = 0, f = 1;
	while(c < '0' || c > '9') {
		if(c == '-') f = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
	return x * f;
}
/*int max_ele(int a,int b,int c,int d){
    if (b>a)
        a = b;
    if (c>a)
        a = c;
    if (d>a)
        a = d;
    return a;
}*/
int  f[51][51][51][51],n,m;
int a[51][51];

signed main() {
	cin>>n>>m;
	for(int i=1; i<=n; ++i)
		for(int j=1; j<=m; ++j)
			cin>>a[i][j];
	for(int i=1; i<=n; ++i) {
		for(int j=1; j<=m; ++j) {
			for(int k=1; k<=n; ++k) {
				for(int l=j+1; l<=m; ++l) {
					f[i][j][k][l]=max(max(f[i][j-1][k-1][l],f[i-1][j][k][l-1] ),max(f[i][j-1][k][l-1],f[i-1][j][k-1][l]) )+a[i][j]+a[k][l];
					//f[i][j][k][l]=max_ele(f[i][j-1][k-1][l],f[i-1][j][k][l-1] ,f[i][j-1][k][l-1],f[i-1][j][k-1][l])+a[i][j]+a[k][l];
				}
			}
		}
	}
	//cout<<f[1][1][n][m];
	cout<<f[n][m-1][n-1][m];
	return 0;
}

这种做法复杂度其实很高了，能过全是题水的原因

做法二:

来自luogu题解第一篇:传送门

因为是从上方和从下方传纸条，为了方便，我们相当于从左上角连续传两张纸条，路径不重复，效果相同。

从左上来看的话就只能向右或向下传纸条。

那么两张纸条在过程中就一定在一条斜线上，而在一条斜线上纵坐标与横坐标相加相等。

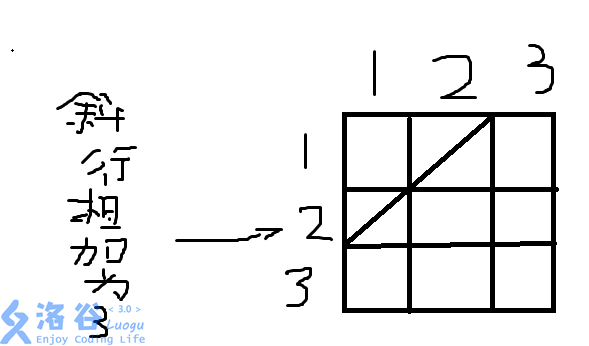
首先重要的就是三维F数组。

第一维度维护的是在传的过程中纵坐标与横坐标的和。

在同一斜线上，剩下表示两个点的从坐标就可以表示这两个点的位置。
第二维度维护的是相对在左边的点的纵坐标。

第三维度维护的是相对在右边的点的纵坐标。

当查询一个情况时，只有四种情况可以到他

F[sum][i][j]=max{F[sum-1][i][j]+F[k-1][i][j-1]+F[k-1][i-1][j]+F[k-1][i-1][j-1]；

最后再加上a数组里存的两个点的好感度即可

include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=60;
int a[maxn][maxn];
int F[2*maxn][maxn][maxn];
int main()
{
  int m,n;
  scanf("%d%d",&m,&n);
  for(int i=1;i<=m;i++)
    for(int j=1;j<=n;j++)
      scanf("%d",&a[i][j]);
  //F[sum][i][j]=max{F[sum-1][i][j]...
  memset(F,-1,sizeof(F));//赋初值为-1 (原因在后面） 
  F[2][1][1]=0;//最初的点，在左上角，好感度为0 
  for(int k=3;k<m+n;k++)
    for(int i=1;i<n;i++)
      for(int j=i+1;j<=n;j++)
      {
        int s=F[k][i][j];
        if(F[k-1][i][j]>s)s=F[k-1][i][j];
        if(F[k-1][i-1][j]>s)s=F[k-1][i-1][j];
        if(F[k-1][i][j-1]>s)s=F[k-1][i][j-1];
        if(F[k-1][i-1][j-1]>s)s=F[k-1][i-1][j-1];
        if(s==-1)continue;//当s为-1时，说明四种情况都不能到该点，故不存在。 
        F[k][i][j]=s+a[k-i][i]+a[k-j][j];//该点的值为最大的前一个值与当前F[k][i][j]表示两点的值的和。 
      }
  printf("%d",F[m+n-1][n-1][n]);//因为i永远小于j，所以右下角的点不会求到，
  //但是到右下角只有一种情况，就是在右下角的上面和右下角的左边，直接输出就好了。 
  return 0;
 } 

类似的题目:

点这里传送