单调队列的原理及其实现

单调队列是一种用来快速查询一段长度为n的数组的一部分的最大最小值的算法。它原理相对简单，且易于实现，并且时间复杂度是接近O(n)的，可以解决很多问题。下面以洛谷P1886滑动窗口 /【模板】单调队列为例来介绍单调队列的实现方法。

先放上题目：

题目描述

有一个长为n的序列a，以及一个大小为k的窗口。现在这个窗口从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1,3,-1,-3,5,3,6,7],and k=3。

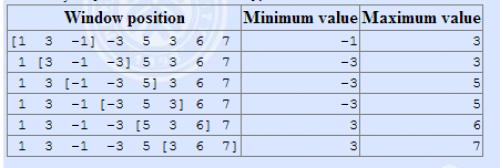
输入格式

输入一共有两行，第一行有两个正整数n,k。第二行n个整数，表示序列a

输出格式

输出共两行，第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值

解法介绍：

单调队列并不使用queue，而只需要在原序列中维护两个边界，分别为l和r，代表研究的部分的左边界位置、右边界位置。我们将左边界的位置初始化为1，右边界的位置初始化为k，代表最初这个研究部分只包含a[1]到a[k]这些节点。此时，我们并不知道这个子区间的最大值和最小值分别是多少，所以我们需要维护一个find函数来寻找子区间内的最大、最小值。这里我们进行一次find初始化，并且对最初的最大值、最小值进行记录。find函数只需要从l到r进行枚举查询即可。

find函数代码实现如下：

 

const int inf=0x3f3f3f3f;
void find(int l,int r){
    maxn=-inf;minn=inf;//初始化最大值和最小值
    for(int i=l;i<=r;i++){
        maxn=max(maxn,a[i]);
        minn=min(minn,a[i]);
    }
}

接下来我们需要对这个窗口进行滑动操作。我们总共需要向右移动(n-k+1)次，每一次都要进行l++，r++的操作。而在操作的时候我们需要维护最值，这也是最为重要的操作。

我们在维护时要分很多种情况：

第一种，也是最好处理的一种情况，当在进行l++操作之前的l所对应的a[l]既不是上一个窗口所对应的最大值，又不是它所对应的最小值时，删去这个值并不会影响窗口内的最大值和最小值，这时候我们可以放心的l++，r++，然后用新加入单调队列的a[r]对maxn和minn进行update更新即可。

代码：

void update(){
  l++;
  r++;
  maxn=max(maxn,a[r]);
  minn=min(minn,a[r]);
}
//接下来是在循环中的判断
if(a[l]!=maxn&&a[l]!=minn){
  update();
} 

第二种，当在进行l++操作之前的l所对应的a[l]是上一个窗口所对应的最大值，而不是它所对应的最小值时，删除a[l]会对新区间内的最大值造成影响，我们已经不知道除了这个被删除掉的节点以外，新窗口的最大值是多少，所以我们要重新查找。但是，这种情况不会对最小值造成影响。但是，如果新加入的节点要大于等于要删除的节点，那么删除掉这个节点也就无所谓了。所以我们还需要加入一个判断：

if(a[l]==maxn){//如果左边界的值等于最大值 
    if(a[r+1]>=a[l]){//新加入节点值大于等于删除的节点 
        update();//不需要重新查找 
    }else{
        l++;
        r++;
        find(l,r);//否则重新查找 
    }
}

第三种，当在进行l++操作之前的l所对应的a[l]是上一个窗口所对应的最小值，而不是它所对应的最大值时，我们可以用与第二种情况相同的方式来查找。代码如下：

if(a[l]==minn){ 
  if(a[r+1]<a[l]){
      update();
  }else{
      l++;
      r++;
      find(l,r);
  }
} 

第四种，也是最为玄学的一种情况，就是当在进行l++操作之前的l所对应的a[l]既是上一个窗口所对应的最小值，又是它所对应的最大值的情况。这种情况下直接重新查找就可以了，毕竟这种情况极少，且考虑起来会很麻烦。

代码：

if(a[l]==maxn&&a[l]==minn){
    l++;
    r++;
    find(l,r);
}

最后附上完整代码：

#include<iostream>
#include<algorithm>
using namespace std;
const int inf=0x3f3f3f3f;
int n,k; 
int l,r;
int a[1000005];
int maxn,minn;
int max_ans[1000005],min_ans[1000005];
void record(int now){
    max_ans[now]=maxn;
    min_ans[now]=minn;
}
void find(int l,int r){
    maxn=-inf;
    minn=inf;
    for(int i=l;i<=r;i++){
        maxn=max(maxn,a[i]);
        minn=min(minn,a[i]);
    }
}
void update(){
    l++;
    r++;
    maxn=max(a[r],maxn);
    minn=min(a[r],minn);
}
int main(){
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    l=1;
    r=k;
    find(l,r);
    for(int i=1;i<=n-k+1;i++){
        record(i);
        if(a[l]!=maxn&&a[l]!=minn){
            update();
        }else if(a[l]==maxn&&a[l]==minn){
            l++;
            r++;
            find(l,r);
        }else if(a[l]==maxn){
            if(a[r+1]>a[l]){
                update();
            }else{
                l++;
                r++;
                find(l,r);
            }
        }else{
            if(a[r+1]<a[l]){
                update();
            }else{
                l++;
                r++;
                find(l,r);
            }
        }
    }
    for(int i=1;i<=n-k+1;i++){
        cout<<min_ans[i]<<' ';
    }
    cout<<endl;
    for(int i=1;i<=n-k+1;i++){
        cout<<max_ans[i]<<' ';
    }
    cout<<endl;
    return 0;
}