Qt版连连看之极速连连看：路线判定算法

【github地址】speedlink-qt

连连看路线判定算法分析

连连看游戏规则：若两个图块相同且它们可以用一条两折之内的折线相连，那么它们消除掉。
用一个二位数组表示连连看的面板，那么每一种图块都可以用一个数字来表示，不同的数字代表不同的图案，0代表没有，消除图案=将该处置为0，这样，游戏的逻辑表示就完成了。
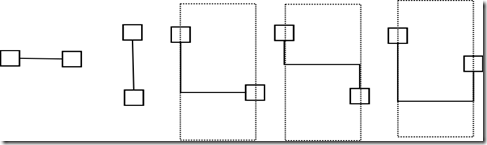
仔细分析连连看的规则，可以发现连连看的连线无非这么几种类型：直连型、一折型、两折型，它们大致的线型有如图：

仔细观察图，就可以发现，虽然两折型稍微复杂，但是观察一下就可以发现，如果将这两个点分别看成一个矩形两条平行边上的两点，这个矩形的另外两条边最大延伸到面板的边界，如果这两点是可连的，那么必定有一条线段可以连通这两条平行边，而且两点分别可以直线连通这条线段的两个端点。这种见解虽然没错，却不太方便实现，如果再观察一下，如果将其中一点为中心画一个十字，那么只要在这个十字上找到一点，这一点可以与另外一点以不多于一个折点相连，这就足以概括几乎所有的情况，因此实现了“判定一个点与另一个点可以使用一个折点相连“就可以了。

为什么不使用简单的回溯呢？如果使用上面的方法，寻路算法的复杂度要远远低于回溯，由于连连看中图块位置随机，不能定量分析，在此不仔细分析其复杂度。在实践中发现，如果使用回溯的方法，那么对于死局判定这种比较耗时的操作，往往游戏时就会稍微“卡”一下，对于小型设备则更是影响游戏流畅度，因此不使用回溯。

算法实现：

bool 
DrawArea::isPosLinkable(int x1_,int y1_,int x2_,int y2_,
                            int *nPos,Pos *pos1,Pos *pos2)
{
    assert(isValid(x1_,y1_));
    assert(isValid(x2_,y2_));
    
    bool posFlag=false;//传入参数中是否有折点
    if(nPos){
        posFlag=true;
        if(!(pos1&&pos2))
            return false;
    }
    
    int x1=x1_;
    int x2=x2_;
    int y1=y1_;
    int y2=y2_;
    if(!isSame(x1,y1,x2,y2))
        return false;
        
    //First,check whether they can be directly linked
    if(isLineLinkable(x1,y1,x2,y2)){
        if(posFlag) *nPos=0;
        
        return true;
    }
    //Second,check whether they can be linked with one turning
    if(findInteractPoint(x1,y1,x2,y2)){
        if(posFlag){
            *nPos=1;
            pos1->x=x2;
            pos1->y=y2;
        }
        return true;
    }
    //Third,check x-direct point that can be linked with one turning
    for(int i=0;i<xMax;++i){
        if(isBlank(i,y1) && 
           isLineLinkable(i,y1,x1,y1) && 
           findInteractPoint(i,y1,x2,y2)){
               if(posFlag){
                    *nPos=2;
                    pos1->x=i;
                    pos1->y=y1;
                    pos2->x=x2;
                    pos2->y=y2;
                }
            return true;
        }
    }
    //Fourth,check y-direct point that can be linked with one turning
    for(int i=0;i<yMax;++i){
        if(isBlank(x1,i) && 
           isLineLinkable(x1,i,x1,y1) && 
           findInteractPoint(x1,i,x2,y2)){
               if(posFlag){
                    *nPos=2;
                    pos1->x=x1;
                    pos1->y=i;
                    pos2->x=x2;
                    pos2->y=y2;
                }
            return true;
        }
    }
    return false;
}
/* 
 * 寻找以 (x1,y1)和 (x2,y2)所在线段为对角线的矩形中对这两个点均可直线到达的顶点
 * 若找到，则将 (x2,y2)改写为该顶点，否则，返回false
 */
bool 
DrawArea::findInteractPoint(const int &x1,const int &y1,int &x2,int &y2)
{
    if(!board[x1][y2]){
        if(isLineLinkable(x1,y1,x1,y2) &&
            isLineLinkable(x2,y2,x1,y2)){
            x2=x1;
            return true;
        }
    }
    if(!board[x2][y1]){
            if(isLineLinkable(x1,y1,x2,y1)&&
                isLineLinkable(x2,y2,x2,y1)){
                y2=y1;
                return true;
            }
    }
    return false;
}
/*
 * 检验两点是否可以直线无障碍到达
 */
bool 
DrawArea::isLineLinkable(int x1,int y1,int x2,int y2)
{
    if(x1 == x2){
        if(y1>y2)    std::swap(y1,y2);
        
        for(y1+=1;y1<y2;++y1)
            if(board[x1][y1])
                return false;
            
    }else if(y1 == y2){
        if(x1>x2)    std::swap(x1,x2);
        
        for(x1+=1;x1<x2;++x1)
            if(board[x1][y1])
                return false;
    }else
        return false;
    
    return true;
}

死局判断就容易多了，布局完成之后，以及每次销块结束之后进行一次判定即可。因为游戏还要有提示功能，在做遍历寻找可消块过程中把找到的第一对可销块记录作为提示之用就可以了。（由于我的游戏中创造了“上帝模式”，进入死局时，提示块为任意一对相同图案的图块。）

死局判断及提示块记录：

/* 判断是否已经进入死局，死局条件：
 * 在回合尚未结束的情况下遍历面板，无法找到一对可销图块
 * 则判定为死局。若找到一对可销图块，则将其记录为hintA
 * 和hintB,以供hint()函数利用。
 */
bool
DrawArea::isDead()
{
    int i,j,x,y;
    if(!pairLeft)
        return true;
    for(i=0;i<xMax;++i){
        for(j=0;j<yMax;++j){
            if(board[i][j]){
                for(x=i;x<xMax;++x){
                    if(x==i)    y=j+1;
                    else y=0;
                    
                    for(;y<yMax;++y){
                        if(board[x][y]==board[i][j]){
                            if(isPosLinkable(i,j,x,y)){//如果消块成功，那么这里就变成了0
                                hintA.x=i;
                                hintA.y=j;
                                hintB.x=x;
                                hintB.y=y;
                                return false;
                            }
                        }
                    }
                }
            }
        }
    }
    return true;
}