一个简单的离散傅里叶变换公式如下面所示
X(k) = ∑<N>x(n)e-j2πkn/N, k = 0,1,2```N-1
傅里叶变换用于分析时域信号中的频域成分,即从时域信号x(n)得到频域信号X(k)
这里的∑<N>表示对求和项从n=0加到N-1,为N点傅里叶变换,输入时域信号为N个,输出频域信号也为N个
看一个简单的例子
x(t) = sin(2π*1000*t) + 0.5sin(2π*2000*t+3*π/4)
它由一个1kHz的信号和一个2kHz的信号组成,频率成分非常明显,所以我们能一眼看出,而有些信号则不是那么明显,则可以借助傅里叶变换来求出频率成分
此处以该简单例子验证,也可以说是做一个简单的傅里叶变换的演示。
为了对该信号进行处理,我们需要对它进行采样,假设采样频率为fs=8kHz,以n为采样得到的值的索引,并以此为变量重新表示上述信号为
x(n) = sin(2π*1000*n/8000) + 0.5sin(2π*2000*n/8000+3*π/4)
并设N=8即做8个点的DFT变换,下面我们将借助MATLAB工具进行计算和演示
首先我们使用MATLAB画出x(t)的波形,如下图
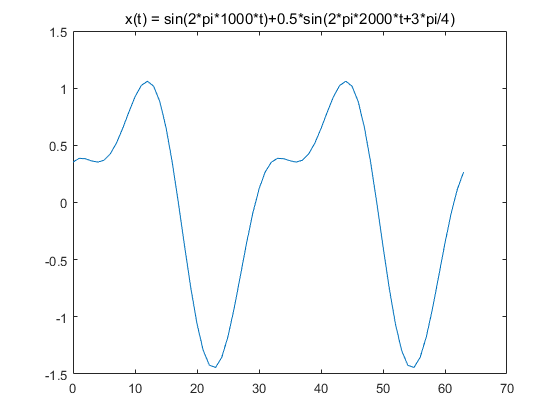
图中x轴的数字为我为了绘制该波形所用到的信号的个数,不要与时间单位秒对应,知道这里显示了两个周期的信号即可
下面再给出一组8点DFT输入信号的图示
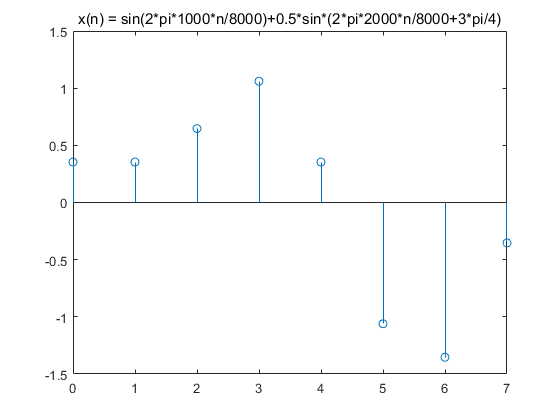
图中的8个点即我们使用8倍于信号周期(8kHz)采样所得到的一个周期的样本,利用这8个数据,我们便可以利用DFT求得其频率成分
在MATLAB中,直接调用FFT并将结果用图形显示如下,FFT为计算DFT的一种快速算法,其结果和直接使用DFT是一样的
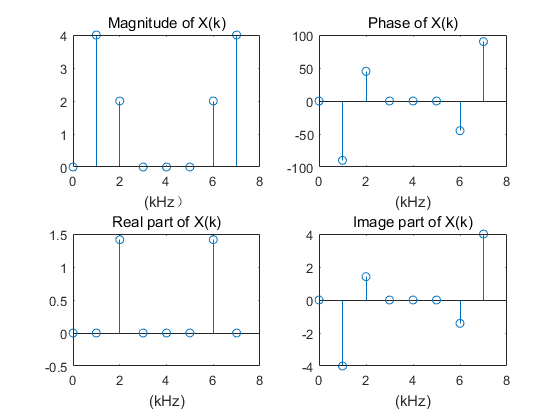
如上图,我们可以看到,计算的结果和我们已知吻合。计算得到信号中有1kHz和2kHz的频率成分,且幅值前者为后者两倍
这里有个小点,上面4个图除了其中一个都是由FFT的计算结果直接绘制的,由于MATLAB对于0的表示,或者说是机器计算原本应该是0的值,它得到了一个很小的值(这很正常),所以用调用angle函数求得的相位是不正确的,
我直接根据正确的结果而绘制了相位图
关于频域信号的单位,很简单,采样率为fs的信号做N点DFT,所得到的频域信号单位为
fanalysis(k) = k*fs/N
对于我们的例子,fs为8kHz,N为8,则对应X(k)当k为0时为直流量,k为1时为1kHz频率成分,依此类推
从上图我们还可以看到X(k)信号具有某种对称性,准确的关系为
X(k) = X(k+N/2)*
即X(k)与X(k+N/2)共轭,也就是说,对于N点频域信号,只有N/2个点的信号是独立的
所以虽然从图中看出好像是有6kHz和7kHz的信号成分,但实际上是不存在的,这也符合奈奎斯特采样定理,采样频率必须大于两倍的信号频率,从侧面反应出用8kHz去采样最多只能采到4kHz以内的信号
所以我们可以看到,采样率和做几个点的DFT运算很关键,假设我们让N=4,则就得不到1kHz频率成分的情况
最后再解释频域幅值大小与时域幅值大小的关系,这里我们的输入信号为实数信号,对应频域幅值为时域幅值的N/2倍
写在最后,刚刚接触信号处理,写点东西整理下思路。文中的例子来自Lyons的Understanding Digital Signal Processing,这是一本很不错的教材,强烈推荐