1 最熟悉的陌生人:多重共线性

逆矩阵存在的充分必要条件

行列式不为0的充分必要条件







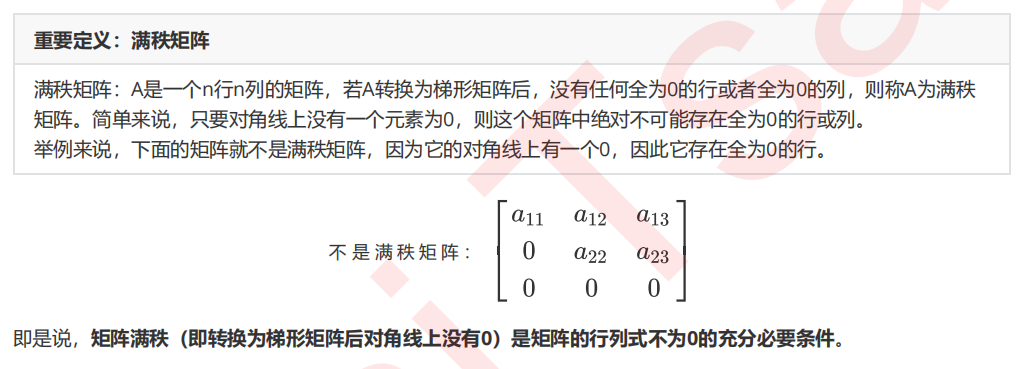
矩阵满秩的充分必要条件




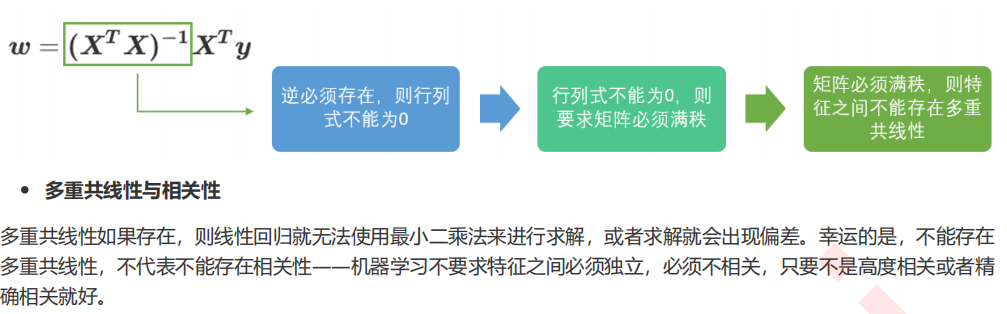




2 岭回归
2.1 岭回归解决多重共线性问题







2.2 linear_model.Ridge

import numpy as np import pandas as pd from sklearn.linear_model import Ridge, LinearRegression, Lasso from sklearn.model_selection import train_test_split as TTS from sklearn.datasets import fetch_california_housing as fch import matplotlib.pyplot as plt housevalue = fch() X = pd.DataFrame(housevalue.data) y = housevalue.target X.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目" ,"平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"] X.head() Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420) #数据集索引恢复 for i in [Xtrain,Xtest]: i.index = range(i.shape[0]) #使用岭回归来进行建模 reg = Ridge(alpha=1).fit(Xtrain,Ytrain) reg.score(Xtest,Ytest) #交叉验证下,与线性回归相比,岭回归的结果如何变化? alpharange = np.arange(1,1001,100) ridge, lr = [], [] for alpha in alpharange: reg = Ridge(alpha=alpha) linear = LinearRegression() regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean() linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean() ridge.append(regs) lr.append(linears) plt.plot(alpharange,ridge,color="red",label="Ridge") plt.plot(alpharange,lr,color="orange",label="LR") plt.title("Mean") plt.legend() plt.show() #细化一下学习曲线 alpharange = np.arange(1,201,10)

#模型方差如何变化? alpharange = np.arange(1,1001,100) ridge, lr = [], [] for alpha in alpharange: reg = Ridge(alpha=alpha) linear = LinearRegression() varR = cross_val_score(reg,X,y,cv=5,scoring="r2").var() varLR = cross_val_score(linear,X,y,cv=5,scoring="r2").var() ridge.append(varR) lr.append(varLR) plt.plot(alpharange,ridge,color="red",label="Ridge") plt.plot(alpharange,lr,color="orange",label="LR") plt.title("Variance") plt.legend() plt.show()
from sklearn.datasets import load_boston from sklearn.model_selection import cross_val_score X = load_boston().data y = load_boston().target Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420) #先查看方差的变化 alpharange = np.arange(1,1001,100) ridge, lr = [], [] for alpha in alpharange: reg = Ridge(alpha=alpha) linear = LinearRegression() varR = cross_val_score(reg,X,y,cv=5,scoring="r2").var() varLR = cross_val_score(linear,X,y,cv=5,scoring="r2").var() ridge.append(varR) lr.append(varLR) plt.plot(alpharange,ridge,color="red",label="Ridge") plt.plot(alpharange,lr,color="orange",label="LR") plt.title("Variance") plt.legend() plt.show() #查看R2的变化 alpharange = np.arange(1,1001,100) ridge, lr = [], [] for alpha in alpharange: reg = Ridge(alpha=alpha) linear = LinearRegression() regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean() linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean() ridge.append(regs) lr.append(linears) plt.plot(alpharange,ridge,color="red",label="Ridge") plt.plot(alpharange,lr,color="orange",label="LR") plt.title("Mean") plt.legend() plt.show() #细化学习曲线 alpharange = np.arange(100,300,10) ridge, lr = [], [] for alpha in alpharange: reg = Ridge(alpha=alpha) #linear = LinearRegression() regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean() #linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean() ridge.append(regs) lr.append(linears) plt.plot(alpharange,ridge,color="red",label="Ridge") #plt.plot(alpharange,lr,color="orange",label="LR") plt.title("Mean") plt.legend() plt.show()

2.3 选取最佳的正则化参数取值


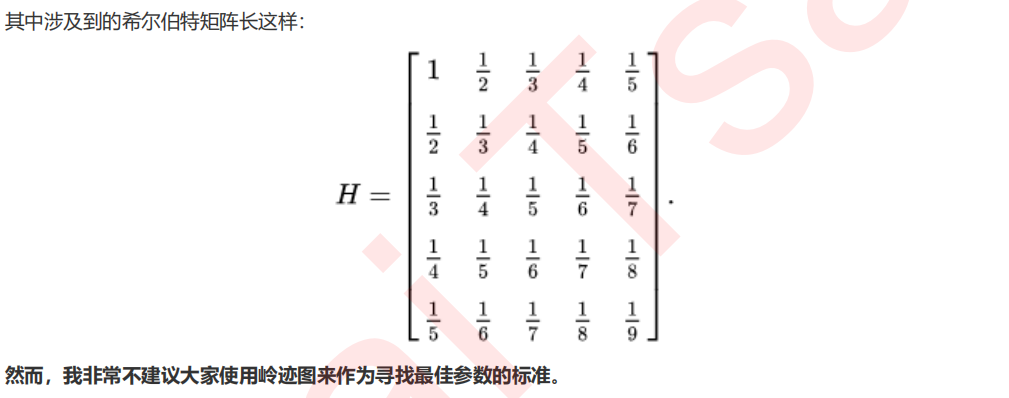
import numpy as np import matplotlib.pyplot as plt from sklearn import linear_model #创造10*10的希尔伯特矩阵 X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis]) y = np.ones(10) #计算横坐标 n_alphas = 200 alphas = np.logspace(-10, -2, n_alphas) #建模,获取每一个正则化取值下的系数组合 coefs = [] for a in alphas: ridge = linear_model.Ridge(alpha=a, fit_intercept=False) ridge.fit(X, y) coefs.append(ridge.coef_) #绘图展示结果 ax = plt.gca() ax.plot(alphas, coefs) ax.set_xscale('log') ax.set_xlim(ax.get_xlim()[::-1]) #将横坐标逆转 plt.xlabel('正则化参数alpha') plt.ylabel('系数w') plt.title('岭回归下的岭迹图') plt.axis('tight') plt.show()



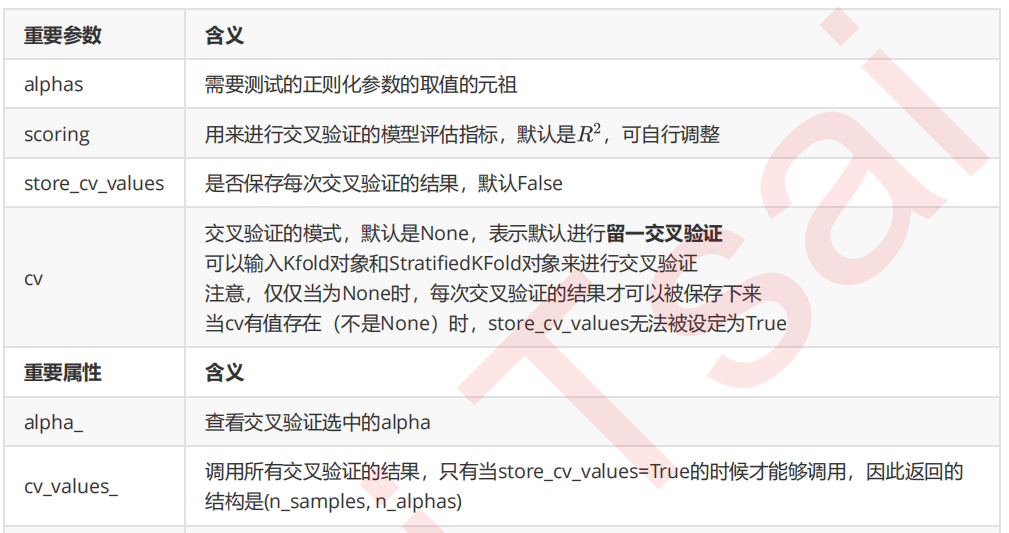

这个类的使用也非常容易,依然使用我们之前建立的加利佛尼亚房屋价值数据集:
import numpy as np import pandas as pd from sklearn.linear_model import RidgeCV, LinearRegression from sklearn.model_selection import train_test_split as TTS from sklearn.datasets import fetch_california_housing as fch import matplotlib.pyplot as plt housevalue = fch() X = pd.DataFrame(housevalue.data) y = housevalue.target X.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目" ,"平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"] Ridge_ = RidgeCV(alphas=np.arange(1,1001,100) #,scoring="neg_mean_squared_error" ,store_cv_values=True #,cv=5 ).fit(X, y) #无关交叉验证的岭回归结果 Ridge_.score(X,y) #调用所有交叉验证的结果 Ridge_.cv_values_.shape #进行平均后可以查看每个正则化系数取值下的交叉验证结果 Ridge_.cv_values_.mean(axis=0) #查看被选择出来的最佳正则化系数 Ridge_.alpha_