机器学习sklearn（81）：算法实例（三十八）回归（十）线性回归大家族（八）非线性问题：多项式回归（三）多项式回归PolynomialFeatures

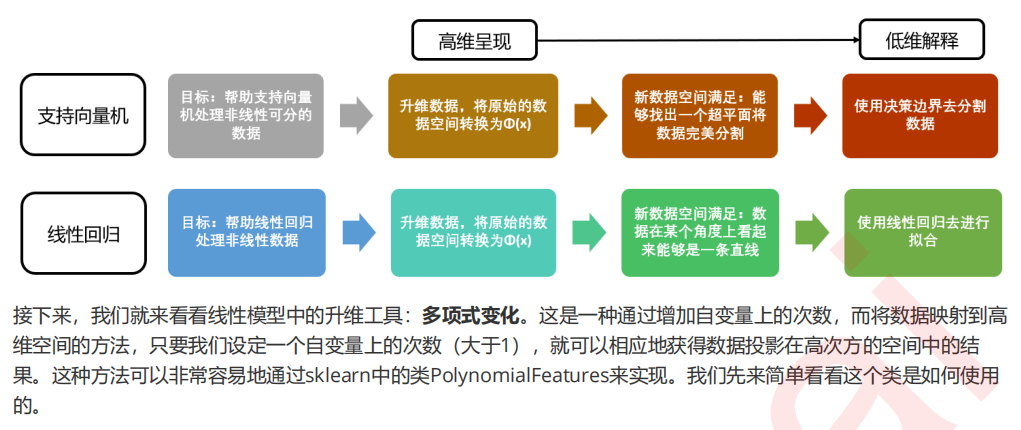
1 多项式对数据做了什么

 

 

from sklearn.preprocessing import PolynomialFeatures
import numpy as np
#如果原始数据是一维的
X = np.arange(1,4).reshape(-1,1) X#二次多项式，参数degree控制多项式的次方
poly = PolynomialFeatures(degree=2) #接口transform直接调用
X_ = poly.fit_transform(X)
X_
X_.shape
#三次多项式
PolynomialFeatures(degree=3).fit_transform(X)

 

 

#三次多项式，不带与截距项相乘的x0
PolynomialFeatures(degree=3,include_bias=False).fit_transform(X) #为什么我们会希望不生成与截距相乘的x0呢？
#对于多项式回归来说，我们已经为线性回归准备好了x0，但是线性回归并不知道
xxx = PolynomialFeatures(degree=3).fit_transform(X)
xxx.shape
rnd = np.random.RandomState(42) #设置随机数种子
y = rnd.randn(3) y#生成了多少个系数？
LinearRegression().fit(xxx,y).coef_
#查看截距
LinearRegression().fit(xxx,y).intercept_
#发现问题了吗？线性回归并没有把多项式生成的x0当作是截距项
#所以我们可以选择：关闭多项式回归中的include_bias
#也可以选择：关闭线性回归中的fit_intercept
#生成了多少个系数？
LinearRegression(fit_intercpet=False).fit(xxx,y).coef_
#查看截距
LinearRegression(fit_intercpet=False).fit(xxx,y).intercept_

X = np.arange(6).reshape(3, 2) 
X
#尝试二次多项式
PolynomialFeatures(degree=2).fit_transform(X)

#尝试三次多项式
PolynomialFeatures(degree=3).fit_transform(X)

PolynomialFeatures(degree=2).fit_transform(X)
PolynomialFeatures(degree=2,interaction_only=True).fit_transform(X) #对比之下，当interaction_only为True的时候，只生成交互项

#更高维度的原始特征矩阵
X = np.arange(9).reshape(3, 3) 
X
PolynomialFeatures(degree=2).fit_transform(X)
PolynomialFeatures(degree=3).fit_transform(X)
X_ = PolynomialFeatures(degree=20).fit_transform(X)
X_.shape

2 多项式回归处理非线性问题

from sklearn.preprocessing import PolynomialFeatures as PF
from sklearn.linear_model import LinearRegression
import numpy as np
rnd = np.random.RandomState(42) #设置随机数种子
X = rnd.uniform(-3, 3, size=100) y = np.sin(X) + rnd.normal(size=len(X)) / 3 #将X升维，准备好放入sklearn中 X = X.reshape(-1,1) #创建测试数据，均匀分布在训练集X的取值范围内的一千个点
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1) #原始特征矩阵的拟合结果
LinearR = LinearRegression().fit(X, y) #对训练数据的拟合
LinearR.score(X,y) #对测试数据的拟合
LinearR.score(line,np.sin(line))
#多项式拟合，设定高次项
d=5 #进行高此项转换
poly = PF(degree=d)
X_ = poly.fit_transform(X)
line_ = PF(degree=d).fit_transform(line) #训练数据的拟合
LinearR_ = LinearRegression().fit(X_, y)
LinearR_.score(X_,y) #测试数据的拟合
LinearR_.score(line_,np.sin(line))

如果我们将这个过程可视化：

import matplotlib.pyplot as plt
d=5 #和上面展示一致的建模流程
LinearR = LinearRegression().fit(X, y)
X_ = PF(degree=d).fit_transform(X)
LinearR_ = LinearRegression().fit(X_, y)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
line_ = PF(degree=d).fit_transform(line) #放置画布
fig, ax1 = plt.subplots(1) #将测试数据带入predict接口，获得模型的拟合效果并进行绘制
ax1.plot(line, LinearR.predict(line), linewidth=2, color='green'
         ,label="linear regression")
ax1.plot(line, LinearR_.predict(line_), linewidth=2, color='red'
         ,label="Polynomial regression") #将原数据上的拟合绘制在图像上
ax1.plot(X[:, 0], y, 'o', c='k') #其他图形选项
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Linear Regression ordinary vs poly")
plt.tight_layout()
plt.show()
#来一起鼓掌，感叹多项式回归的神奇
#随后可以试试看较低和较高的次方会发生什么变化
#d=2
#d=20

3 多项式回归的可解释性 

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
X = np.arange(9).reshape(3, 3) X
poly = PolynomialFeatures(degree=5).fit(X) #重要接口get_feature_names
poly.get_feature_names()

from sklearn.datasets import fetch_california_housing as fch
import pandas as pd
housevalue = fch()
X = pd.DataFrame(housevalue.data) y = housevalue.target
housevalue.feature_names
X.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目"
           ,"平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]
poly = PolynomialFeatures(degree=2).fit(X,y)
poly.get_feature_names(X.columns)
X_ = poly.transform(X) #在这之后，我们依然可以直接建立模型，然后使用线性回归的coef_属性来查看什么特征对标签的影响最大
reg = LinearRegression().fit(X_,y)
coef = reg.coef_
[*zip(poly.get_feature_names(X.columns),reg.coef_)]
#放到dataframe中进行排序
coeff = pd.DataFrame([poly.get_feature_names(X.columns),reg.coef_.tolist()]).T
coeff.columns = ["feature","coef"]
coeff.sort_values(by="coef")

#顺便可以查看一下多项式变化之后，模型的拟合效果如何了
poly = PolynomialFeatures(degree=4).fit(X,y)
X_ = poly.transform(X)
reg = LinearRegression().fit(X,y)
reg.score(X,y)
from time import time
time0 = time()
reg_ = LinearRegression().fit(X_,y)
print("R2:{}".format(reg_.score(X_,y)))
print("time:{}".format(time()-time0))
#假设使用其他模型？
from sklearn.ensemble import RandomForestRegressor as RFR
time0 = time()
print("R2:{}".format(RFR(n_estimators=100).fit(X,y).score(X,y)))
print("time:{}".format(time()-time0))

4 线性还是非线性模型？

 

 

https://stats.stackexchange.com/questions/92065/why-is-polynomial-regression-considered-a-special-case-of-multiple-linear-regres