[POJ3233] Matrix Power Series

传送门：>Here<

题意：给出一个$N*N$的矩阵$A$，求$A + A^2 + A^3 + ... A^k$    $（N leq 30, k leq 10^9）$

解题思路

如果仅仅只需要求$A^k$，那么直接一个矩阵快速幂即可，复杂度$O(n^3 log k)$。然而现在要求一个类似前缀和的东西，那么必须想出一个别的方法

考虑一个分块矩阵：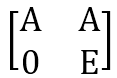

所谓分块矩阵，也就是矩阵的每个元素都是一个子矩阵。其中，E为单位矩阵，0为零矩阵

将此矩阵自乘一次会得到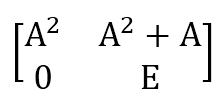

自乘两次会得到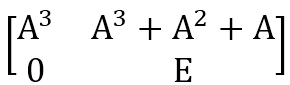

 

因此自乘$K-1$次，取右上角的元素即可。

分块矩阵依然满足矩阵乘法规则。

Code

　　无

/*By DennyQi*/
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm>
#define  r  read()
#define  Max(a,b)  (((a)>(b)) ? (a) : (b))
#define  Min(a,b)  (((a)<(b)) ? (a) : (b))
using namespace std;
typedef long long ll;
const int MAXN = 10010;
const int MAXM = 27010;
const int INF = 1061109567;
inline int read(){
    int x = 0; int w = 1; register int c = getchar();
    while(c ^ '-' && (c < '0' || c > '9')) c = getchar();
    if(c == '-') w = -1, c = getchar();
    while(c >= '0' && c <= '9') x = (x << 3) +(x << 1) + c - '0', c = getchar(); return x * w;
}
int N,K,M;
int A[35][35],a[70][70],ans[70][70],b[70][70];
inline void Matrix_KSM(int y){
    while(y > 0){
        if(y & 1){
            for(int i = 1; i <= 2*N; ++i){
                for(int j = 1; j <= 2*N; ++j){
                    b[i][j] = 0;
                    for(int k = 1; k <= 2*N; ++k){
                        b[i][j] = (b[i][j] + ans[i][k] * a[k][j]) % M;
                    }
                }
            }
            for(int i = 1; i <= 2*N; ++i){
                for(int j = 1; j <= 2*N; ++j){
                    ans[i][j] = b[i][j];
                }
            }
        }
        for(int i = 1; i <= 2*N; ++i){
            for(int j = 1; j <= 2*N; ++j){
                b[i][j] = 0;
                for(int k = 1; k <= 2*N; ++k){
                    b[i][j] = (b[i][j] + a[i][k] * a[k][j]) % M;
                }
            }
        }
        for(int i = 1; i <= 2*N; ++i){
            for(int j = 1; j <= 2*N; ++j){
                a[i][j] = b[i][j];
            }
        }
        y /= 2;
    }
}
int main(){
//    freopen(".in","r",stdin);
    N=r,K=r,M=r;
    for(int i = 1; i <= N; ++i){
        for(int j = 1; j <= N; ++j){
            A[i][j] = r;
            a[i][j] = A[i][j];
            a[i][j+N] = A[i][j];
        }
    }
    for(int i = N+1; i <= 2*N; ++i){
        a[i][i] = 1;
    }
    for(int i = 1; i <= 2*N; ++i){
        ans[i][i] = 1;
    }
    Matrix_KSM(K);
    for(int i = 1; i <= N; ++i){
        for(int j = N+1; j <= 2*N; ++j){
            printf("%d ", ans[i][j]);
        }
        printf("
");
    }
    return 0;
}