欲知前情如何,请看第十届福建工程学院校赛赛题。
小A和小C正在私奔的路上,遇到一个前来追赶他们的特工,然而这个特工明显是个临时工,三下五除二就把特工打晕了,缴获了一部手机。小A和小C想要通过这个特工的手机获取情报,而这台手机有图案密码锁。大概由于这个特工比较健忘,手机的密码提示写了一排数字,小A根据数字滑动密码锁,却不能打开。
小C说:“是不是要换个顺序才能打开?”
小A觉得很有道理,但是这个情况数好像很多的样子,然而小A是个聪明的程序员,他有足够的信心破解这个手机图案密码。
现在小A已经知道手机图案锁是只由哪几个位置组成的,手机图案锁的解锁只能通过一笔画解决,他最多需要多少次情况就一定能够破解该图案锁的密码?每个位置必须经过,每个位置只能够被经过一次。
图案锁的组成有9个位置分别为:
1 2 3
4 5 6
7 8 9
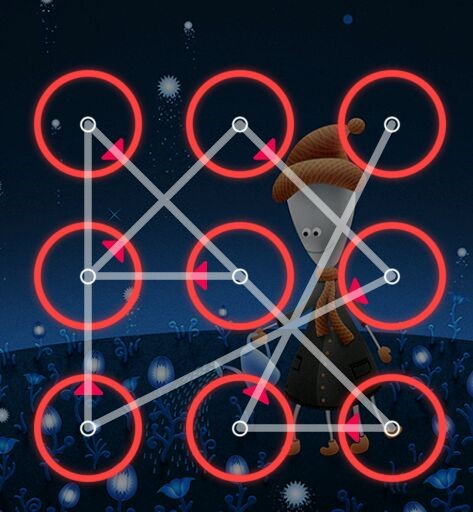
如上图所示:
会提示你密码包含1,2,3,4,5,6,7,8,9.
其中的一种画法如上图:5->4->2->6->7->1->9->8->3.
经过小A多次研究,发现以下规律:
如果你还没有经过5, 然后 你连接了1, 再去连接9的话, 则会经过5.
如果你已经经过5, 然后你连接1, 再去连接9的话, 则不会在重新经过5.
同理可得1和3、4和6等也满足如上规律。
有多组测试案例.
每一组测试案例的第一行输入一个整数N(1<=N<=9),表示图案锁由N个密码组成。
接下来输入N个数值,表示这N密码的位置。
输出最多需要多少次便能够解锁,如果不能够解锁,请输出-1。
1 1 2 1 9 2 1 5 3 1 5 9
1 -1 2 4
【思路】:这个题目其实就是一个深度优先搜索
DFS
就是类似一棵树,看他能不能走到底,如图:
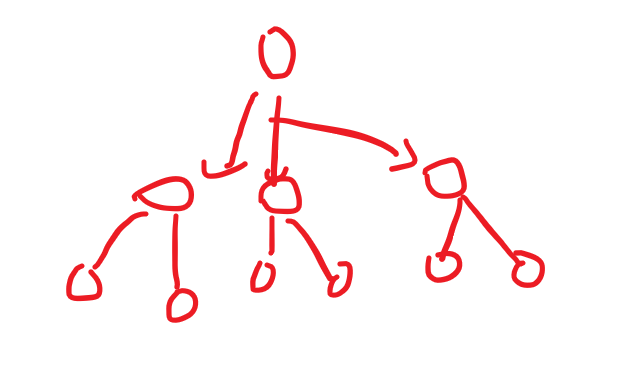
这题就是判断能不能把走到最后一层,可以的话,就加一。不可以就不用管了,
然后应该用标记法,标记走过的地方,然后在递归返回的时候再把其重置,可以让下次不同方向的搜索,
重复使用,但是这题有一些特殊的情况,暴力枚举就可以了。
#include<stdio.h> #include<string.h> int math[15]; int flag[15]; int ans[15]; int n; int sum; void dfs(int t) {int i; if(t==n) { sum++; return; } for(i=0; i<n; i++) { if(flag[math[i]]==0) {if(t!=0) { if(flag[5]==0&&ans[t-1]==1&&math[i]==9)continue; if(flag[5]==0&&ans[t-1]==9&&math[i]==1)continue; if(flag[5]==0&&ans[t-1]==2&&math[i]==8)continue; if(flag[5]==0&&ans[t-1]==8&&math[i]==2)continue; if(flag[5]==0&&ans[t-1]==3&&math[i]==7)continue; if(flag[5]==0&&ans[t-1]==7&&math[i]==3)continue; if(flag[5]==0&&ans[t-1]==4&&math[i]==6)continue; if(flag[5]==0&&ans[t-1]==6&&math[i]==4)continue; if(flag[2]==0&&ans[t-1]==1&&math[i]==3)continue; if(flag[2]==0&&ans[t-1]==3&&math[i]==1)continue; if(flag[4]==0&&ans[t-1]==1&&math[i]==7)continue; if(flag[4]==0&&ans[t-1]==7&&math[i]==1)continue; if(flag[6]==0&&ans[t-1]==3&&math[i]==9)continue; if(flag[6]==0&&ans[t-1]==9&&math[i]==3)continue; if(flag[8]==0&&ans[t-1]==7&&math[i]==9)continue; if(flag[8]==0&&ans[t-1]==9&&math[i]==7)continue; } ans[t]=math[i]; flag[math[i]]=1; dfs(t+1); flag[math[i]]=0; } } } int main() { int i; while(~scanf("%d",&n)) { sum=0; memset(flag,0,sizeof(flag)); for(i=0; i<n; i++) { scanf("%d",&math[i]); } dfs(0); if(sum!=0) printf("%d ",sum); if(sum==0) printf("-1 "); } return 0; }
