- 题库 : 洛谷
- 题号 : 1262
- 题目 : 间谍网络
- link : https://www.luogu.org/problemnew/show/P1262
思路 :
这题可以用缩点的思想来做。先用Tarjan算法以一个没有被搜过&&能被收贿赂的点为起点,把每个强连通分量给缩成一个点(一个强连通分量 )(这个强连通分量里的任意一个可以收贿赂的间谍 收贿赂之后,就可以 掌握这个强连通分量中其他间谍的证据),然后我们在搜Tarjan 的时候记得把每个强连通分量中的最小收贿赂值算出来,这个对以后计算答案很有帮助。
最后就剩下两点了:
- 可以掌握所有间谍的证据 : 这个情况是因为搜完Tarjan之后,所有点都在强连通分量里(至于在哪个无所谓,反正都在强连通分量里)。那 么我们只需要把入度为0的强连通分量中的最小收贿赂 值加起来就好了(如果入度不为0,那么这个强连通分量就可以被其他强连通分 量中的间谍掌握证据,这样这个强连通分量就都可以不用收贿赂就被掌握证据了)
- 不能掌握所有间谍的证据 : 这个情况是因为当我们搜完Tanjan之后,如果有一个点(间谍)没有被搜到过,他就无法被掌握证据(他不在任何 一个强连通分量中,他既无法被收贿赂,也无法被其 他能收贿赂的间谍掌握证据)。
注意 :
你可能会怀疑一个强连通分量中没有任何一个间谍可以收贿赂,当然,这种情况是有的。但如果一个强连通分量被搜到了&&他里面没有可以收 贿赂的间谍,既然他被搜到了,那么一定有一个可以 收贿赂的间谍出 发,最后搜到了当前强连通分量(这个强连通分量的入度肯定不为0, 所以这个担心是多余的)
解释一下样例:
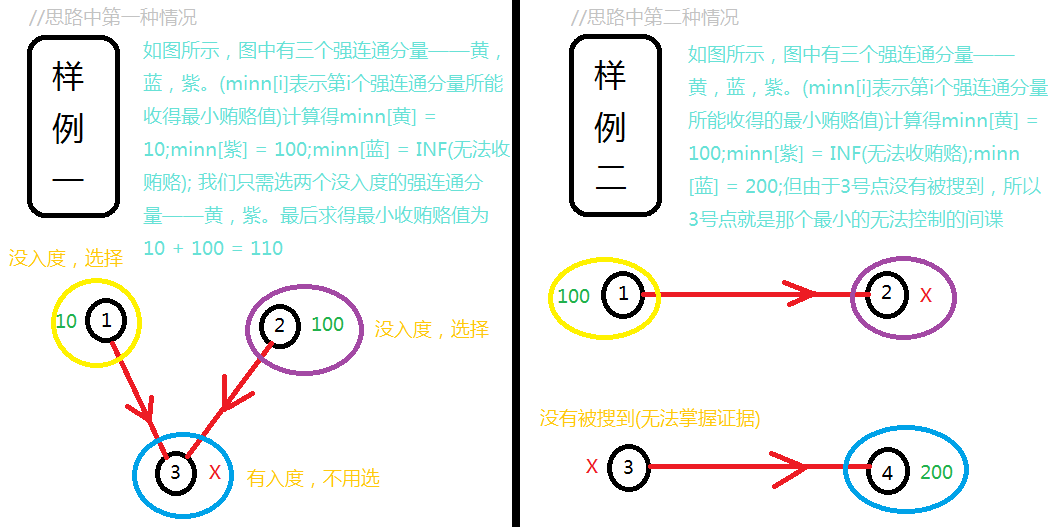
code :
1 #include <bits/stdc++.h> 2 #define INF 0x3f3f3f3f 3 using namespace std; 4 stack < int > pru; 5 int n, m, M, q[100001], dfn[100001], low[100001], vis[100001], col[100001], head[100001], minn[100001], in[100001], color, num, z, ans; 6 struct node 7 { 8 int next, to; 9 }stu[100001]; 10 inline void add(int x, int y)//链表存图 11 { 12 stu[++num].next = head[x]; 13 stu[num].to = y; 14 head[x] = num; 15 return; 16 } 17 inline void tarjan(int u)//Tarjan模板 18 { 19 dfn[u] = low[u] = ++z; 20 vis[u] = 1; 21 pru.push(u); 22 for(register int i = head[u]; i; i = stu[i].next) 23 { 24 int k = stu[i].to; 25 if(!vis[k]) 26 { 27 tarjan(k); 28 low[u] = min(low[u], low[k]); 29 } 30 else if(!col[k]) 31 { 32 low[u] = min(low[u], dfn[k]); 33 } 34 } 35 if(dfn[u] == low[u]) 36 { 37 col[u] = ++color; 38 minn[color] = min(minn[color], q[u]);//在一个强连通分量中,寻找其中可以贿赂的最小值 39 while(pru.top() != u) 40 { 41 col[pru.top()] = color; 42 minn[color] = min(minn[color], q[pru.top()]);//同理 43 pru.pop(); 44 } 45 pru.pop(); 46 } 47 return; 48 } 49 signed main() 50 { 51 memset(minn, INF, sizeof(minn));//初始化为最大 52 memset(q, INF, sizeof(q));//同理 53 scanf("%d %d", &n, &M); 54 for(register int i = 1, x, y; i <= M; ++i) 55 { 56 scanf("%d %d", &x, &y); 57 q[x] = y; 58 } 59 scanf("%d", &m); 60 for(register int i = 1, x, y; i <= m; ++i) 61 { 62 scanf("%d %d", &x, &y); 63 add(x, y); 64 } 65 for(register int i = 1; i <= n; ++i) 66 { 67 if(!vis[i] && q[i] != INF)//要判断这人是否可以贿赂 68 { 69 tarjan(i); 70 } 71 } 72 for(register int i = 1; i <= n; ++i) 73 { 74 if(!vis[i])//如果有人没被搜到过(及无法掌握这人的证据) 75 { 76 printf("NO %d", i);//由于是从小到大(1 ~ n),所以第一个搜到没被搜过的就是最小值 77 return 0; 78 } 79 } 80 for(register int u = 1; u <= n; ++u) 81 { 82 for(register int i = head[u]; i; i = stu[i].next)//寻找其中入度为0的点 83 { 84 int k = stu[i].to; 85 if(col[k] != col[u])//颜色不同(及不在一个强连通分量中) 86 { 87 ++in[col[k]];//k所在的强连通分量的入度++ 88 } 89 } 90 } 91 for(register int i = 1; i <= color; ++i)//枚举每个强连通分量 92 { 93 if(!in[i])//没有入度(不能被其他强连通分量中的间谍掌握证据) 94 { 95 ans += minn[i];//这个点中可收贿赂最小的间谍就必须贿赂他 96 } 97 } 98 printf("YES %d", ans); 99 return 0; 100 }