Codeforces Round #296 (Div. 1) C. Data Center Drama 欧拉回路

Codeforces Round #296 (Div. 1)C. Data Center Drama

Time Limit: 2 Sec Memory Limit: 256 MB
Submit: xxx Solved: 2xx

题目连接

http://codeforces.com/contest/528/problem/C

Description

The project of a data center of a Big Software Company consists of n computers connected by m cables. Simply speaking, each computer can be considered as a box with multiple cables going out of the box. Very Important Information is transmitted along each cable in one of the two directions. As the data center plan is not yet approved, it wasn't determined yet in which direction information will go along each cable. The cables are put so that each computer is connected with each one, perhaps through some other computers.

The person in charge of the cleaning the data center will be Claudia Ivanova, the janitor. She loves to tie cables into bundles using cable ties. For some reasons, she groups the cables sticking out of a computer into groups of two, and if it isn't possible, then she gets furious and attacks the computer with the water from the bucket.

It should also be noted that due to the specific physical characteristics of the Very Important Information, it is strictly forbidden to connect in one bundle two cables where information flows in different directions.

The management of the data center wants to determine how to send information along each cable so that Claudia Ivanova is able to group all the cables coming out of each computer into groups of two, observing the condition above. Since it may not be possible with the existing connections plan, you are allowed to add the minimum possible number of cables to the scheme, and then you need to determine the direction of the information flow for each cable (yes, sometimes data centers are designed based on the janitors' convenience...)

Input

The first line contains two numbers, n and m (1 ≤ n ≤ 100 000, 1 ≤ m ≤ 200 000) — the number of computers and the number of the already present cables, respectively.

Each of the next lines contains two numbers a_i, b_i (1 ≤ a_i, b_i ≤ n) — the indices of the computers connected by the i-th cable. The data centers often have a very complex structure, so a pair of computers may have more than one pair of cables between them and some cables may connect a computer with itself.

Output

In the first line print a single number p (p ≥ m) — the minimum number of cables in the final scheme.

In each of the next p lines print a pair of numbers c_i, d_i (1 ≤ c_i, d_i ≤ n), describing another cable. Such entry means that information will go along a certain cable in direction from c_i to d_i.

Among the cables you printed there should be all the cables presented in the original plan in some of two possible directions. It is guaranteed that there is a solution where p doesn't exceed 500 000.

If there are several posible solutions with minimum possible value of p, print any of them.

Sample Input

Input

Input

Sample Output

Output

Output

HINT

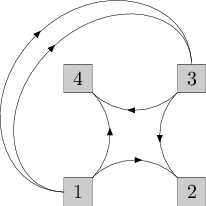
Picture for the first sample test. The tied pairs of cables are shown going out from the same point.

$\text{[math]}$

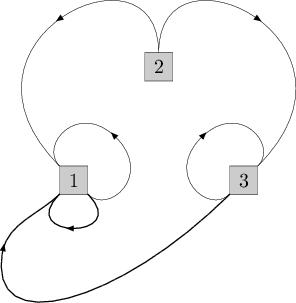
Picture for the second test from the statement. The added cables are drawin in bold.

$\text{[math]}$

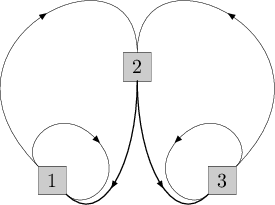
Alternative answer for the second sample test:

$\text{[math]}$

题意：

就是给你一个无向图，然后这些无向图的边，可以转化成一个有向图的边，问你怎么加最少的边，使得每一个点的出度等于入度，输出边数和边集

题解：

首先，我们把所有的无向边都建好，然后如果某一个点的出度是奇数的话，那么我们就依次连接奇数的点

比如 1,2,3的出度是奇数，那么我们就连 1->2,2->3,3->1，这样子就修正好了，就全是偶数啦

然后我们就DFS，来构造欧拉回路！

然后就乌拉拉的跑就是了，如果跑完还是奇数的话，那就随便给一个点加一个自环就好啦~

~(≧▽≦)/~啦啦啦，这道题完啦

代码：

//qscqesze
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
typedef long long ll;
using namespace std;
//freopen("D.in","r",stdin);
//freopen("D.out","w",stdout);
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define maxn 500001
#define mod 10007
#define eps 1e-9
//const int inf=0x7fffffff;   //无限大
const int inf=0x3f3f3f3f;
/*

*/
//**************************************************************************************

inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,m;
multiset<int> e[maxn];
int out[maxn];
int cnt=0;
int a[maxn];
int all;
int ans[maxn];
void dfs(int x)
{
    while(!e[x].empty())
    {
        int i=*(e[x].begin());
        e[x].erase(e[x].begin());
        e[i].erase(e[i].find(x));
        dfs(i);
    }
    ans[++all]=x;
}
int main()
{
    n=read(),m=read();
    while(m--)
    {
        int x=read(),y=read();
        e[x].insert(y);
        e[y].insert(x);
        out[x]++;
        out[y]++;
        cnt++;
    }
    int tot=0;
    for(int i=1;i<=n;i++)
    {
        if(out[i]%2==1)
            a[++tot]=i;
    }
    for(int i=1;i<tot;i+=2)
    {
        e[a[i]].insert(a[i+1]);
        e[a[i+1]].insert(a[i]);
        cnt++;
    }
    if(cnt%2)
        cnt++;
    printf("%d
",cnt);
    all=0;
    dfs(1);
    for(int i=1;i<all;i++)
    {
        if(i%2)
            printf("%d %d
",ans[i],ans[i+1]);
        else
            printf("%d %d
",ans[i+1],ans[i]);
    }
    if(all%2==0)
        printf("1 1
");
}