D. Duff in Beach
Time Limit: 1 Sec
Memory Limit: 256 MB
题目连接
http://codeforces.com/contest/588/problem/D
Description
While Duff was resting in the beach, she accidentally found a strange array b0, b1, ..., bl - 1 consisting of l positive integers. This array was strange because it was extremely long, but there was another (maybe shorter) array, a0, ..., an - 1 that b can be build from a with formula: bi = ai mod n where a mod b denoted the remainder of dividing a by b.

Duff is so curious, she wants to know the number of subsequences of b like bi1, bi2, ..., bix (0 ≤ i1 < i2 < ... < ix < l), such that:
- 1 ≤ x ≤ k
- For each 1 ≤ j ≤ x - 1,
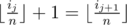
- For each 1 ≤ j ≤ x - 1, bij ≤ bij + 1. i.e this subsequence is non-decreasing.
Since this number can be very large, she want to know it modulo 109 + 7.
Duff is not a programmer, and Malek is unavailable at the moment. So she asked for your help. Please tell her this number.
Input
The first line of input contains three integers, n, l and k (1 ≤ n, k, n × k ≤ 106 and 1 ≤ l ≤ 1018).
The second line contains n space separated integers, a0, a1, ..., an - 1 (1 ≤ ai ≤ 109 for each 0 ≤ i ≤ n - 1).
Output
Sample Input
3 5 3
5 9 1
Sample Output
10
HINT
题意
给你n,l,k,然后就是告诉你b有l长度,其中是由a不停重复得到的
然后问你一共有多少个满足条件的序列存在
条件如下:
1.这个序列的长度大于等于1,小于等于k
2.这个序列在每一个块中只能选择一个数,并且都必须选择在连续的块中
3.这个序列是单调不降的
题解:
dp,由于n*k<=1e6,所以我们简单的推断是dp[n][k]的,表示第i个数长度为k的序列有多少个
其实这道题和分块差不多,在块外就用dp瞎转移
块内就暴力就好了……
只要把这个数据过了就好了
3 100 3
1 1 1
注意是upper_bound这个东西
代码:
#include<stdio.h> #include<iostream> #include<algorithm> #include<map> using namespace std; #define maxn 1000005 #define mod 1000000007 int a[maxn]; int b[maxn]; long long l; int k,n; long long dp[maxn]; long long sum[maxn]; map<int,int> HH; map<pair<int,int>,int> H; int tot = 1; int get(int x,int y) { if(H[make_pair(x,y)]) return H[make_pair(x,y)]; H[make_pair(x,y)]=tot++; return H[make_pair(x,y)]; } int main() { scanf("%d%lld%d",&n,&l,&k); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); b[i]=a[i]; } sort(a+1,a+1+n); for(int i=1;i<=n;i++) HH[a[i]] = i; for(int i=1;i<=n;i++) dp[get(i,1)]=1; for(int j=2;j<=k;j++) { int tot = 1; for(int i=1;i<=n;i++) { int kk = upper_bound(a+1,a+n+1,a[i])-(a+1); while(tot<=kk) { sum[j-1] += dp[get(tot,j-1)]; sum[j-1] %= mod; tot++; } dp[get(i,j)] = sum[j-1]; } } for(int i=1;i<=n;i++) { sum[k] += dp[get(i,k)]; sum[k] %= mod; } long long ans = 0; for(int i=1;i<=k&&i<=l/n;i++) { ans += (long long)((l/n-i+1)%mod)*sum[i]; ans %= mod; } if(l%n==0) { cout<<ans<<endl; return 0; } for(int i=1;i<=l%n;i++) { for(int j=1;j<=k&&j<=(l/n+1);j++) { ans+=dp[get(HH[b[i]],j)]; ans%=mod; } } cout<<ans<<endl; }