Blue

Blue 是个动物学家，不仅喜欢研究猫和老鼠，还喜欢研究青蛙。

他最近开始研究青蛙过河的问题，可以简化成：数轴上0为岸边，L为河对岸。(0,L)中间存在 n 个石子。已知青蛙一跳可以跳距离D，而且不能沾水。求问能不能跳到河对岸。当然他觉得这个问题非常 naïve，于是在思考如果青蛙有 m个，且石头被踩过之后就会沉下去，m个青蛙还能不能依次安全过河。如果不能则问最多能有多少个过河。

输入

第一行为一个正整数T代表数据组数。每组数据第一行四个正整数：n、m、D、L第二行 n 个升序正整数 ai代表第 i个石子坐标为 ai。保证没有重复且都小于L。

输出

TT行”Excited”代表全部能过河或者一个整数代表有多少个能过河的。

对于 10%的数据保证 m=1.

对于另外 10%的数据保证 D=L.

对于另外 10%的数据保证 n=L-1.

对于另外 30%的数据保证 n<=100, L<=10^5.

对于 100%的数据保证 m<=n<=10^6,D<=L<=10^9.

数据范围中的 n、m 皆代表题目描述中 n、m 的总和。

SAMPLE

INPUT

5

10 9 16 30

2 4 6 9 11 15 18 19 25 27

10 1 23 30

10 11 13 14 15 16 18 26 27 29

10 7 28 30

2 3 7 9 12 15 20 24 27 28

10 3 18 30

1 6 9 14 18 19 22 27 28 29

10 7 10 30

1 2 4 6 18 19 20 22 23 26

OUTPUT

5

Excited

Excited

Excited

0

---

思路：

画个图其实就出来了（考试手懒没画……） 

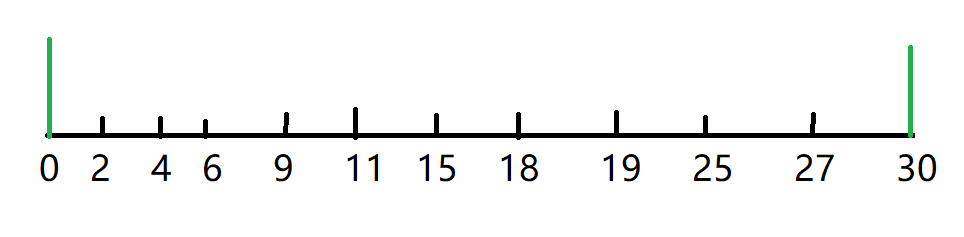
很显然的结论，最多只有k个 (pos[i+k]-pos[i]>=d) 只青蛙可以过河

因为最远可以跳到的石头之前的石头一定是站满的（青蛙足够多）

所以我们只需要枚举每个石头的最远距离就可以啦~

code

#include<stdio.h> 
#include<algorithm> 
using namespace std;
const int mxn=1e6+10;
int n,m,d,L,pos[mxn];

inline int In() {
    int s=0,f=1;
    char ch=getchar();
    while(ch<'0' || ch>'9') {
        if(ch=='-') f=-1;ch=getchar();
    }
    while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
    return s*f;
}

void Sol() {
    pos[0]=0,pos[n+1]=L;
    int ans=m,now=0;
    for(int i=0;i<=n;++i) {
        while(now!=n+1 && pos[now+1]-pos[i]<=d) now++;
        if(i==now) {
            printf("0
");return;
        }
        if(now==n+1) break;
        ans=min(ans,now-i);
    }
    if(ans==m) printf("Excited
");
    else printf("%d
",ans);
}

void file() {
    freopen("blue.in","r",stdin);
    freopen("blue.out","w",stdout);
}

int main() 
{
//    file();
    int T=In();
    while(T--) {
        n=In(),m=In(),d=In(),L=In();
        for(int i=1;i<=n;++i) pos[i]=In();
        if(d>=L) {
            printf("Excited
");continue;
        }
        Sol();
    }
    return 0;
}
/*
5
10 9 16 30
2 4 6 9 11 15 18 19 25 27
10 1 23 30
10 11 13 14 15 16 18 26 27 29
10 7 28 30
2 3 7 9 12 15 20 24 27 28
10 3 18 30
1 6 9 14 18 19 22 27 28 29
10 7 10 30
1 2 4 6 18 19 20 22 23 26
*/