遗传算法GA

1.介绍

以下介绍转自sjyan在知乎的回答，如何通俗易懂地解释遗传算法？有什么例子？

1.介绍

遗传算法(Genetic Algorithm)遵循『适者生存』、『优胜劣汰』的原则，是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。遗传算法模拟一个人工种群的进化过程，通过选择(Selection)、交叉(Crossover)以及变异(Mutation)等机制，在每次迭代中都保留一组候选个体，重复此过程，种群经过若干代进化后，理想情况下其适应度达到***近似最优***的状态。自从遗传算法被提出以来，其得到了广泛的应用，特别是在函数优化、生产调度、模式识别、神经网络、自适应控制等领域，遗传算法发挥了很大的作用，提高了一些问题求解的效率。

2.遗传算法组成

• 编码 -> 创造染色体
• 个体 -> 种群
• 适应度函数
• 遗传算子
  
  • 选择
  • 交叉
  • 变异
• 运行参数
  
  • 是否选择精英操作
  • 种群大小
  • 染色体长度
  • 最大迭代次数
  • 交叉概率
  • 变异概率

2.1 编码与解码

实现遗传算法的第一步就是明确对求解问题的编码和解码方式。对于函数优化问题，一般有两种编码方式，各具优缺点

• 实数编码：直接用实数表示基因，容易理解且不需要解码过程，但容易过早收敛，从而陷入局部最优
• 二进制编码：稳定性高，种群多样性大，但需要的存储空间大，需要解码且难以理解

对于求解函数最大值问题，我选择的是二进制编码。

以我们的目标函数 f(x) = x + 10sin(5x) + 7cos(4x), x∈[0,9] 为例。假如设定求解的精度为小数点后4位，可以将x的解空间划分为 (9-0)×(1e+4)=90000个等分。2^16<90000<2^17，需要17位二进制数来表示这些解。换句话说，一个解的编码就是一个17位的二进制串。一开始，这些二进制串是随机生成的。一个这样的二进制串代表一条染色体串，这里染色体串的长度为17。对于任何一条这样的染色体chromosome，如何将它复原(解码)到[0,9]这个区间中的数值呢？对于本问题，我们可以采用以下公式来解码：

x = 0 + decimal(chromosome)×(9-0)/(2^17-1)

decimal( ): 将二进制数转化为十进制数一般化解码公式：

f(x), x∈[lower_bound, upper_bound]
x = lower_bound + decimal(chromosome)×(upper_bound-lower_bound)/(2^chromosome_size-1)

lower_bound: 函数定义域的下限upper_bound: 函数定义域的上限chromosome_size: 染色体的长度通过上述公式，我们就可以成功地将二进制染色体串解码成[0,9]区间中的十进制实数解。

2.2 个体与种群

『染色体』表达了某种特征，这种特征的载体，称为『个体』。对于本次实验所要解决的一元函数最大值求解问题，个体可以用上一节构造的染色体表示，一个个体里有一条染色体。许多这样的个体组成了一个种群，其含义是一个一维点集(x轴上[0,9]的线段)。

2.3 适应度函数

遗传算法中，一个个体(解)的好坏用适应度函数值来评价，在本问题中，f(x)就是适应度函数。适应度函数值越大，解的质量越高。适应度函数是遗传算法进化的驱动力，也是进行自然选择的唯一标准，它的设计应结合求解问题本身的要求而定。

2.4 遗传算子

我们希望有这样一个种群，它所包含的个体所对应的函数值都很接近于f(x)在[0,9]上的最大值，但是这个种群一开始可能不那么优秀，因为个体的染色体串是随机生成的。如何让种群变得优秀呢？不断的进化。每一次进化都尽可能保留种群中的优秀个体，淘汰掉不理想的个体，并且在优秀个体之间进行染色体交叉，有些个体还可能出现变异。种群的每一次进化，都会产生一个最优个体。种群所有世代的最优个体，可能就是函数f(x)最大值对应的定义域中的点。如果种群无休止地进化，那总能找到最好的解。但实际上，我们的时间有限，通常在得到一个看上去不错的解时，便终止了进化。对于给定的种群，如何赋予它进化的能力呢？

• 首先是选择(selection)
  
  • 选择操作是从前代种群中选择***多对***较优个体，一对较优个体称之为一对父母，让父母们将它们的基因传递到下一代，直到下一代个体数量达到种群数量上限
  • 在选择操作前，将种群中个体按照适应度从小到大进行排列
  • 采用轮盘赌选择方法（当然还有很多别的选择方法），各个个体被选中的概率与其适应度函数值大小成正比
  • 轮盘赌选择方法具有随机性，在选择的过程中可能会丢掉较好的个体，所以可以使用精英机制，将前代最优个体直接选择
• 其次是交叉(crossover)
  
  • 两个待交叉的不同的染色体(父母)根据交叉概率(cross_rate)按某种方式交换其部分基因
  • 采用单点交叉法，也可以使用其他交叉方法
• 最后是变异(mutation)
  
  • 染色体按照变异概率(mutate_rate)进行染色体的变异
  • 采用单点变异法，也可以使用其他变异方法

一般来说，交叉概率(cross_rate)比较大，变异概率(mutate_rate)极低。像求解函数最大值这类问题，我设置的交叉概率(cross_rate)是0.6，变异概率(mutate_rate)是0.01。因为遗传算法相信2条优秀的父母染色体交叉更有可能产生优秀的后代，而变异的话产生优秀后代的可能性极低，不过也有存在可能一下就变异出非常优秀的后代。这也是符合自然界生物进化的特征的。

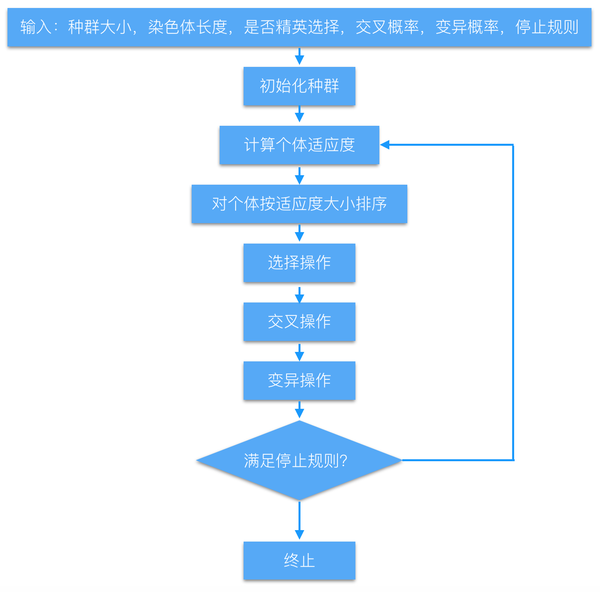
3.遗传算法流程

2.收敛性

转自楚兴的博文遗传算法。

遗传算法的优点：
1. 与问题领域无关切快速随机的搜索能力。
2. 搜索从群体出发，具有潜在的并行性，可以进行多个个体的同时比较，robust.
3. 搜索使用评价函数启发，过程简单
4. 使用概率机制进行迭代，具有随机性。
5. 具有可扩展性，容易与其他算法结合。
 
遗传算法的缺点： 
1. 遗传算法的编程实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码,
2. 另外三个算子的实现也有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验.
3. 没有能够及时利用网络的反馈信息,故算法的搜索速度比较慢，要得要较精确的解需要较多的训练时间。
4. 算法对初始种群的选择有一定的依赖性，能够结合一些启发算法进行改进。
5. 算法的并行机制的潜在能力没有得到充分的利用，这也是当前遗传算法的一个研究热点方向。
在现在的工作中，遗传算法（1972年提出）已经不能很好的解决大规模计算量问题，它很容易陷入“早熟”。常用混合遗传算法，合作型协同进化算法等来替代，这些算法都是GA的衍生算法。

目前已有证明，基本遗传算法只能概率性全局收敛。后续还有NSGA（非支配排序遗传算法）、NSGAII（带精英策略的非支配排序的遗传算法）等算法，都是基于遗传算法的多目标优化算法，都是基于pareto最优解讨论的多目标优化。

3. 实现

选取函数为f(x)=10*np.sin(5*x) + 7*np.cos(4*x)，最大值为17，在[0,10)上有两个最大值点，一个在(1,2)，一个在(7,8)。

不增加额外的计算量，使得扩增之后种群数量不变。

迭代50次，大多数时候能得到16.99999999的结果，偶尔也会16.99999981。

# coding: utf8
import numpy as np

N=20  # 编码长度
MAX=10.0/(2**(N))  # [0,10), 区间内有两个最大值（17）的点
NUM=500  # 种群数量

def f(x):  # 函数
    return 10*np.sin(5*x) + 7*np.cos(4*x)

def new(num=NUM,len=N):  # 随机生成
    return np.random.randint(1,2**len,num)

def n2b(nums):  # 数字编码
    return [bin(i)[2:].zfill(N) for i in nums]

def b2n(bits):  # 解码
    return [int(i,base=2) for i in bits]

def fit(nums,s_rate=0.15,r_rate=0.05):  # 适应度和选择
    n=len(nums)
    sn=int(n*s_rate)
    on=int(n*r_rate)
    np.random.shuffle(nums)
    outs=nums[:on]
    res=[f(i*MAX) for i in nums]   # 适应度选择和随机选择，可能有重复
    temp=np.argsort(res)
    others=[nums[i] for i in temp[-sn:]]
    outs=np.concatenate((outs, others))
    return outs,nums[temp[-1]]*MAX,res[temp[-1]]

def repo(fits):  # 扩增，此处5倍
    n=len(fits)
    pt=np.random.randint(0,n,4*n)
    pt=np.reshape(pt,(2*n,2))
    bits=n2b(fits)
    new_bits=bits
    for i in pt:
        b1,b2=exchange([bits[j] for j in i])
        new_bits.append(b1)
        new_bits.append(b2)
    return mut(new_bits)

def exchange(bits,change_rate=0.4,mode='cross'):  #交换，提供了随机交换和节点互换
    n=int(change_rate*N)
    if mode=='rand':
        rn=range(N)
        new_bits=[list(i) for i in bits]
        for i in rn[:n]:
            new_bits[0][i] = bits[1][i]
            new_bits[1][i] = bits[0][i]
        new_bits=[''.join(i) for i in new_bits]
    else:
        n = int(change_rate * N)
        new_bits = [list(i) for i in bits]
        new_bits[0][:n] = bits[1][:n]
        new_bits[1][:n] = bits[0][:n]
        new_bits = [''.join(i) for i in new_bits]
    return new_bits

def mut(bits,mut_rate=0.03):  # 变异
    length=len(bits)*N
    n = int(mut_rate * length)
    if n<1: n=1
    rn = range(length)
    np.random.shuffle(rn)
    for i in rn[:n]:
        j=int(bits[i/N][i%N])
        bits[i/N]=swap(bits[i/N],i%N,str(1-j))
    return bits

def swap(str,i,char):  # 字符串交换
    str2=list(str)
    str2[i]=char
    return ''.join(str2)

def train(iter=50):  # 训练入口
    nums=new()
    outs,x,fx=fit(nums)
    for i in range(iter):
        new_bits = repo(outs)
        nums=b2n(new_bits)
        outs,x,fx=fit(nums)
        print i,x,fx


if '__main__==main()':
    train()

"""
0 1.57063484192 16.99999528
1 7.85397529602 16.9999999927
2 7.85397529602 16.9999999927
3 7.85397529602 16.9999999927
4 7.85397529602 16.9999999927
5 7.85397529602 16.9999999927
6 1.57079696655 16.9999999999
7 1.57079696655 16.9999999999
8 1.57079696655 16.9999999999
9 1.57079696655 16.9999999999
10 1.57079696655 16.9999999999
11 1.57079696655 16.9999999999
12 1.57079696655 16.9999999999
13 1.57079696655 16.9999999999
14 1.57079696655 16.9999999999
15 1.57079696655 16.9999999999
16 1.57079696655 16.9999999999
17 1.57079696655 16.9999999999
18 1.57079696655 16.9999999999
19 1.57079696655 16.9999999999
20 1.57079696655 16.9999999999
21 1.57079696655 16.9999999999
22 1.57079696655 16.9999999999
23 1.57079696655 16.9999999999
24 1.57079696655 16.9999999999
25 1.57079696655 16.9999999999
26 1.57079696655 16.9999999999
27 1.57079696655 16.9999999999
28 1.57079696655 16.9999999999
29 1.57079696655 16.9999999999
30 1.57079696655 16.9999999999
31 1.57079696655 16.9999999999
32 1.57079696655 16.9999999999
33 1.57079696655 16.9999999999
34 1.57079696655 16.9999999999
35 1.57079696655 16.9999999999
36 1.57079696655 16.9999999999
37 1.57079696655 16.9999999999
38 1.57079696655 16.9999999999
39 1.57079696655 16.9999999999
40 1.57079696655 16.9999999999
41 1.57079696655 16.9999999999
42 1.57079696655 16.9999999999
43 1.57079696655 16.9999999999
44 1.57079696655 16.9999999999
45 1.57079696655 16.9999999999
46 1.57079696655 16.9999999999
47 1.57079696655 16.9999999999
48 1.57079696655 16.9999999999
49 1.57079696655 16.9999999999

"""

4.NSGA非支配排序遗传算法

NSGA与简单的遗传算法的主要区别在于:该算法在选择算子执行之前根据个体之间的支配关系进行了分层。其选择算子、交叉算子和变异算子与简单遗传算法没有区别。
NSGA采用的非支配分层方法，可以使好的个体有更大的机会遗传到下一代;适应度共享策略则使得准Pareto面上的个体均匀分布，保持了群体多样性，克服了超级个体的过度繁殖，防止了早熟收敛。 

Pareto占优

 

Pareto最优解

对于多目标优化问题，通常存在一个解集，这些解之间就全体目标函数而言是无法比较优劣的。

其特点是:无法在改进任何目标函数的同时不削弱至少一个其他目标函数。这种解称作非支配解或Pareto最优解。

Pareto最优前沿

对于组成Pareto最优解集的所有Pareto最优解，其对应目标空间中的目标矢量所构成的曲面称作Pareto最优前沿。