本题征求翻译。如果你能提供翻译或者题意简述,请 提交翻译 ,感谢你的贡献。
题目描述

输入输出格式
输入格式:
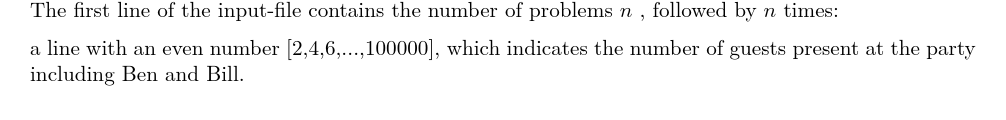
输出格式:

输入输出样例
题解
这个本来是黄题被我打了个绿之后就变成绿题了哈哈哈哈哈哈哈
为了方便想我们设一共有$2n$个人,每种汉堡有$n$个。
>以下错解
>那么前$2n-2$个人中间必须要恰好有$n$个人选了一种汉堡,$n-2$个人选了另一种汉堡。
>那么就很好写啦,$ans=C_{2n-2}^{n}/2^{2n-2}$!
>然后发现n=3的样例都过不了qwq
>然后我跟队友YY分析出了原因:
>如果到第$i$个人的时候已经选了$n$个汉堡的话,那么它之后的选择概率就会从$frac{1}{2}$变成$1$,这样直接把$2^{2n-2}$当方案数就会错掉qwq
怎么办呢?
考虑求后两个人能吃到不一样的汉堡的概率。
那么$now=C_{2n-2}^{n-1}/2^{2n-2}$!
这样我们只选到了$n-1$,就能保证每次选择的概率是$frac{1}{2}$了qwq
最后容斥一下,$ans=1-now$就好了。
.
然后代码为了精度做了一些奇怪操作,总之就是求那个式子的就是了qwq
1 qwerta 2 UVA557 Burger Accepted 3 代码 C++,0.37KB 4 提交时间 2018-10-27 20:29:35 5 耗时/内存 2620ms, 0KB 6 #include<iostream> 7 #include<cstdio> 8 using namespace std; 9 int main() 10 { 11 int t; 12 scanf("%d",&t); 13 while(t--) 14 { 15 int n; 16 scanf("%d",&n); 17 n/=2; 18 double ans=1; 19 int tim=2*n-2; 20 for(int i=1;i<=n-1;++i) 21 { 22 ans*=(i+n-1); 23 ans/=i; 24 while(ans>=1&&tim) 25 { 26 ans*=0.5; 27 tim--; 28 } 29 } 30 while(tim) 31 { 32 ans*=0.5; 33 tim--; 34 } 35 printf("%.4f ",1-ans); 36 } 37 return 0; 38 }