题目链接 :http://codeforces.com/contest/821/problem/B
题意 :给出 m 和 b 表示在坐标轴上的一条直线 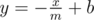 要求你在这条直线和x、y轴围成的区域中找出一个矩形,使得矩形贡献的价值最大,矩形的贡献由在矩形里面的每一个整数点(x, y)的和构成即 x+y。
要求你在这条直线和x、y轴围成的区域中找出一个矩形,使得矩形贡献的价值最大,矩形的贡献由在矩形里面的每一个整数点(x, y)的和构成即 x+y。
分析 :实际就是在一个限定的范围内找价值最大矩阵,那么可以试着枚举在这个区域内的可能有最大贡献的矩阵,根据y从b~0自上而下地枚举,对于每一个yi,我们根据直线方程算出xi(向下取整),那这个xi和yi便确定了在这个y值下可以取到的最大的矩形且矩形右上角是点(xi, yi),应该不难想象,接下来就是计算贡献了,如果暴力计算肯定超时,看看能不能将要计算的点列出来找找规律,如下
y y+1 y+2................y+x
(y-1) (y-1)+1 (y-1)+2.........(y-1)+x
(y-2) (y-2)+1 (y-2)+2.........(y-2)+x
......
0 0+1 0+2.........0+x
可以看出每一行就是一个等差数列,可以利用等差数列公式

#include<bits/stdc++.h> #define LL long long using namespace std; LL m, b; LL cal(LL y){ return (b - y)*m; } LL bananas(LL x, LL y) { LL sum = 0; LL fir = y, last = y+x; LL Firsum = (x+1)*(fir + last)/2; sum += Firsum; for(LL i=1; i<=y; i++){ sum = sum + Firsum - (i*(x+1)); } return sum; } int main(void) { scanf("%lld %lld", &m, &b); LL ans = -1; for(LL y=b; y>=0; y--){ LL x = cal(y); ans = max(ans, bananas(x, y)); } printf("%lld ", ans); return 0; }
实际上,如上是计算还可以更加简便,可以看出每一行的x的和都是一样的,而每一行的y的和也都是一样的,那就可以分开用等差数列计算在乘上个数相加即可,即:

