高精度加法

高精度加法，其实就是long long 都存不下的东西，要算的话，就只能这样做了

不过呢ta有一个麻烦的就是需要把ne特别特别大的数存到数组里，但是数组是左对齐的，而咱们用的小学一年级就会的列竖式大法是右对齐的，这就很气人，所以我们就需要用数组将其转化为右对齐的形式，话不多说，上代码！

for(i=0;i<la;i++)
        a[la-i-1]=sa[i]-'0';
    for(i=0;i<lb;i++)
        b[lb-i-1]=sb[i]-'0';

下一个麻烦就是进位的问题了，像这种数组的类竖式哈，我们就需要用一个变量去存储ta所产生的进位问题，上代码！

//相加+处理进位 
    lc=max(la,lb);
    for(i=0;i<lc;i++){
        c[i]=(a[i]+b[i]+jw)%10;//相加 
        jw=(a[i]+b[i]+jw)/10;//处理进位 
    }

这时候，如果运行代码，比如运算99999+99999，答案应该是1099998，但是。。。

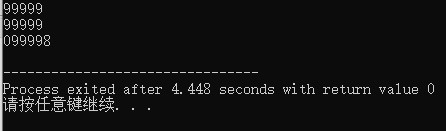
 这。。。就很过分，hhh

所以，我们还要解决最高位置上的进位问题，我们只能当进位这个变量不为0的时候，附到前一位上

上代码！

//处理最高位的进位 
    if(jw!=0){
        lc++;
        c[lc]=jw;
    }

这时候，我们运算一个简单的，02+06，我们都知道，前面这个0就没用，所以答案应该是008，但是计算机不知道啊，ta输出的就成了。。

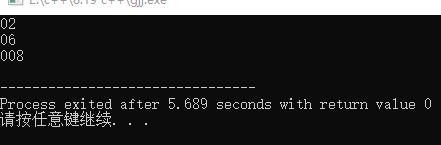
所以，我们就要解决这个多余的0的问题，也比较简单，只需要进行一个特判，只要是0，就减减就ok，也就是把这个位数往右移，像这个008，就应该-2，向右移2位，输出8，就ok了，上代码！

//删除先导0
    while (c[lc] == 0) lc--;

这个时候，加上输出代码就可以了，所以综合起来这么多的“麻烦”后，最后的代码是酱紫的

#include<bits/stdc++.h>
using namespace std;

string sa,sb;
int la,lb,lc,a[1010],b[1010],c[1010],i,jw;

int main(){
    cin>>sa>>sb;
    la=sa.length();
    lb=sb.length();
    
    //输入 
    for(i=0;i<la;i++)
        a[la-i-1]=sa[i]-'0';
    for(i=0;i<lb;i++)
        b[lb-i-1]=sb[i]-'0';
    
    //相加+处理进位 
    lc=max(la,lb);
    for(i=0;i<lc;i++){
        c[i]=(a[i]+b[i]+jw)%10;//相加 
        jw=(a[i]+b[i]+jw)/10;//处理进位 
    }
    
    //处理最高位的进位 
    if(jw!=0){
        lc++;
         c[lc]=jw;
    }
    
    //删除先导0
    while (c[lc] == 0) lc--;
    
    //输出
    if(lc<0)
        cout<<"0";
    else{
        for(i=lc;i>=0;i--)
            cout<<c[i];
        cout<<endl;
    }
    
    return 0; 
}

 学会了之后，可以刷两道题耍耍

试题链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1168