抽屉原理
原理1:
把多于n+1个的物体放到n个抽屉里,则至少有一个抽屉里的东西不少于两件。
证明(反证法):如果每个抽屉至多只能放进一个物体,那么物体的总数至多是n×1,而不是题设的n+k(k≥1),故不可能。
原理2:
把多于mn+1(n不为0)个的物体放到n个抽屉里,则至少有一个抽屉里有不少于(m+1)的物体。
证明(反证法):若每个抽屉至多放进m个物体,那么n个抽屉至多放进mn个物体,与题设不符,故不可能。
原理3:
把无穷多件物体放入n个抽屉,则至少有一个抽屉里有无穷个物体。
原理4:
把(mn-1)个物体放入n个抽屉中,其中必有一个抽屉中至多有(m—1)个物体。
注意
在实际问题中,一般把较多的一方看做物件,较少的一方看做抽屉。
要遵循最差原则,考虑所有可能情况中,最不利于某件事情发生的情况。
例题
1.已知n+ 1个互不相同的正整数,它们全都小于或等于2n,证明当中一定有两个数是互质的。
在这n+1个数中必有两个数是连续数,而连续数是互质的。
2.在一个边长为2厘米的等边三角形内(包括边界)选出5个点,请证明:一定有两个点之间的距离不大于1.
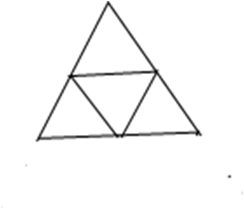
如图所示必定有两个点在一个小三角形里。
3.在一个7X7的方格中,每个小方格内都有一条小虫,在同一时刻方格中的小虫必须向周围(上下左右4个方向)爬一格。
证明:在爬了一格之后,至少有一个小方格是空的

25个黑格,24个白格,小虫只能从白格爬到黑格或从黑格爬到白格,则至少有一个黑格是空的。
加法原理乘法原理
例题
四个不同的小球放入编号为1、2、3、4的四个盒子中,则恰有一个空盒子的放法有多少种?
从四个球中取出2个作为一组,与另两个球一起放入四个盒子中的三个内,有C(4,2)A(4,3) =64!=144种放法。
或将四个球分别放入四只盒子后,取出其中的2合并为一盒,有A(4,4) * C(4,2) =4!*6=144种放法。
排列组合
圆排列
n个里面选r个:A(n, r) / r
例题
有8人围圆桌就餐,问有多少种就座方式?如果有两人不愿坐在一起,又有多少种就座方式?
问一.A(8,8)/8=8!/8=7!(种)
问二.7! - 2×6! = 3600 (种) 2是两个人的排列,6!是8个人里面选两个人看做一个人后(7个人)的圆排列
无限重排列(相异元素可重复排列)
从n个不同元素(可以重复/放回)中取r个元素排列等于nr。
有限重排列(不全相异元素的排列)
n个元素中n1个彼此相同,n2个彼此相同,n3个彼此相同……求全排列
n!/n1!/n2!/n3!/……