泡芙

题目链接

_{如果不是有题解一辈子都调不出来}

tarjan

题目中说“这条路就不能再走了”所以是不能缩点嘛……？

看这张图

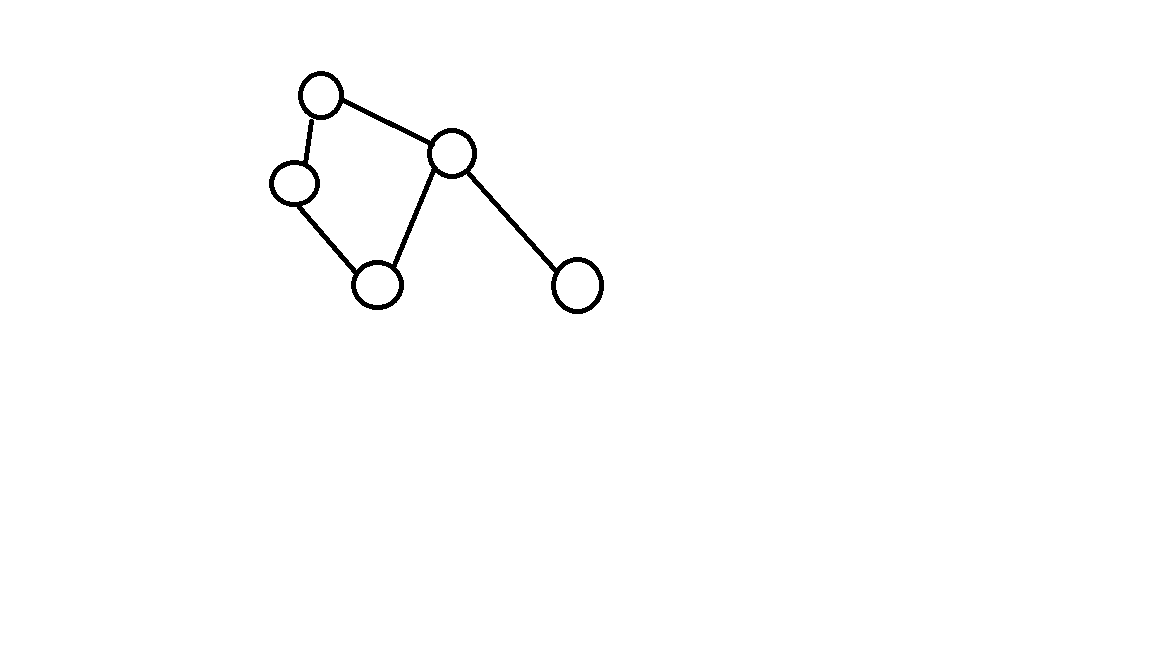
会发现从环里的点出发走一圈正好是可以走回来的！可以缩点！

tips：边不能重复走可以缩点，点不能重复走不能缩点

注意实际处理与一般情况稍有区别，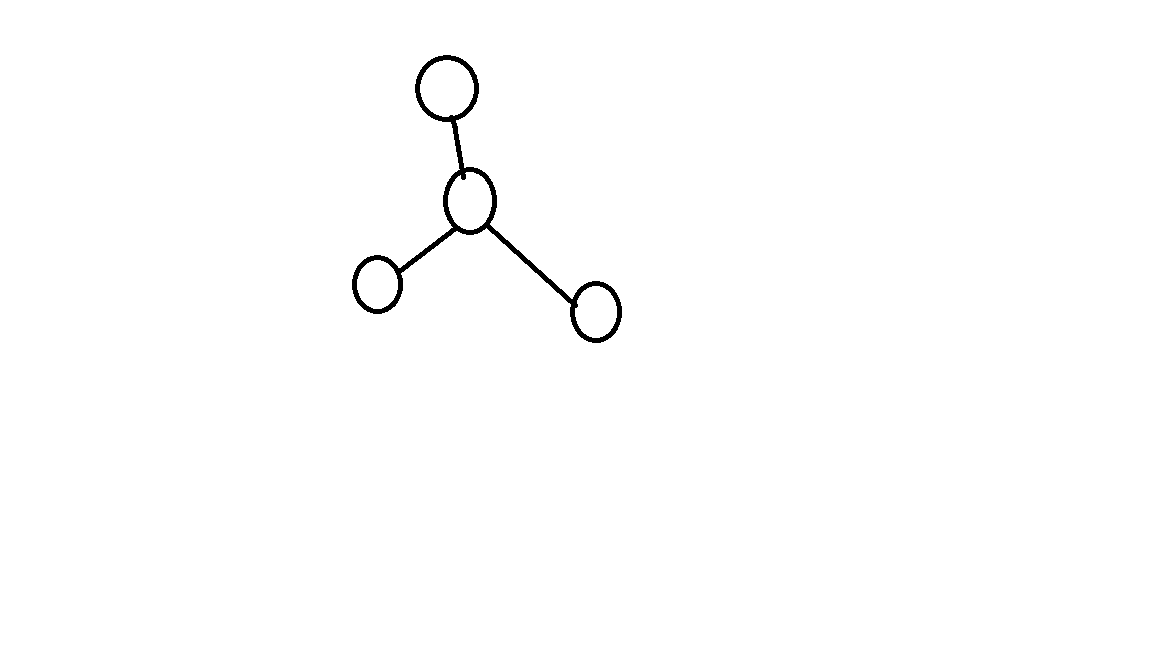

在这张图中，一般情况下会作为一个强连通分量，但是因为边不能重复，所以它们其实不能绕一圈绕回来，怎么办？

特判，不直接向父亲节点转移，因为从父亲到儿子这条边已经走过了，再转移就走重了

如果有重边呢（原题中并没有说明有没有重边自环）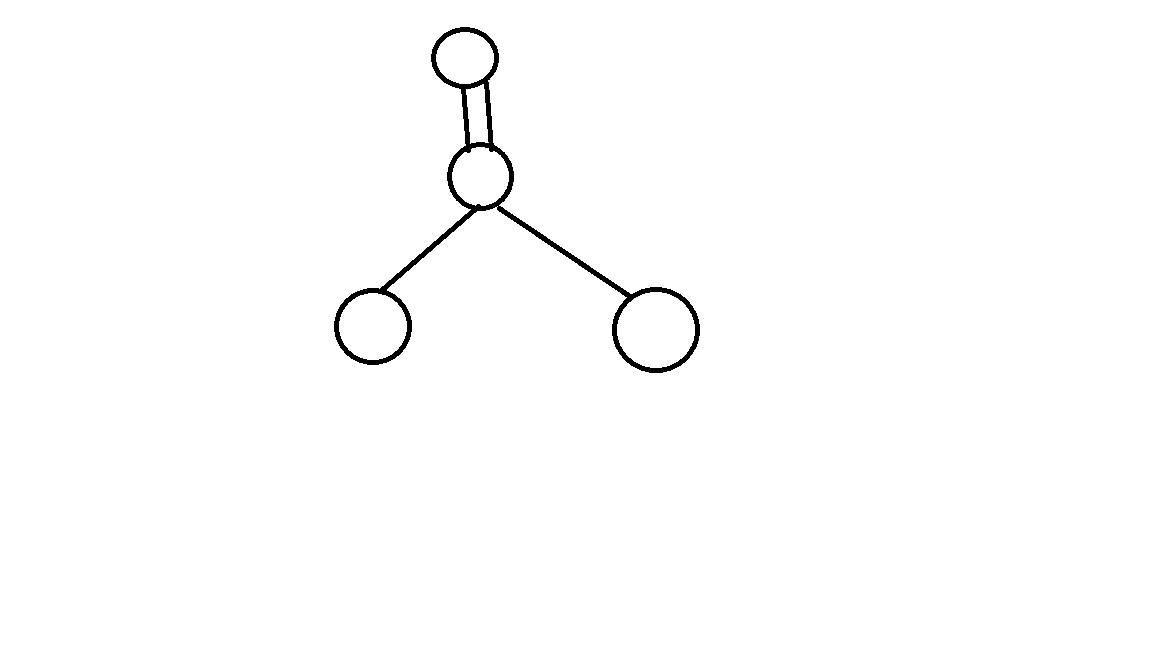

明明是一个强连通分量但是却不会缩点

可以改为特判边有没有走过，也可以当成多个点处理，不影响

lca

缩完点是dag！爆搜！，，，然而t了

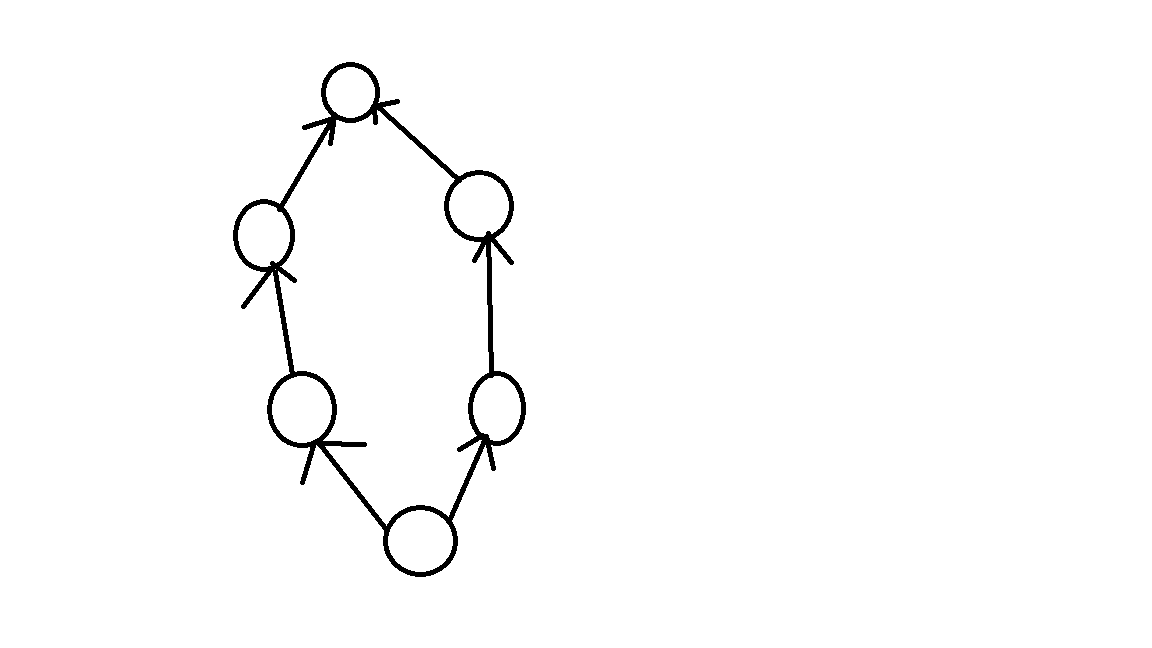
看这张图，这是dag然而不是树

同样是有向无环，但是dag图中一个点可以有多个前继，而树只能有一个爸爸

但是如果是无向图呢？

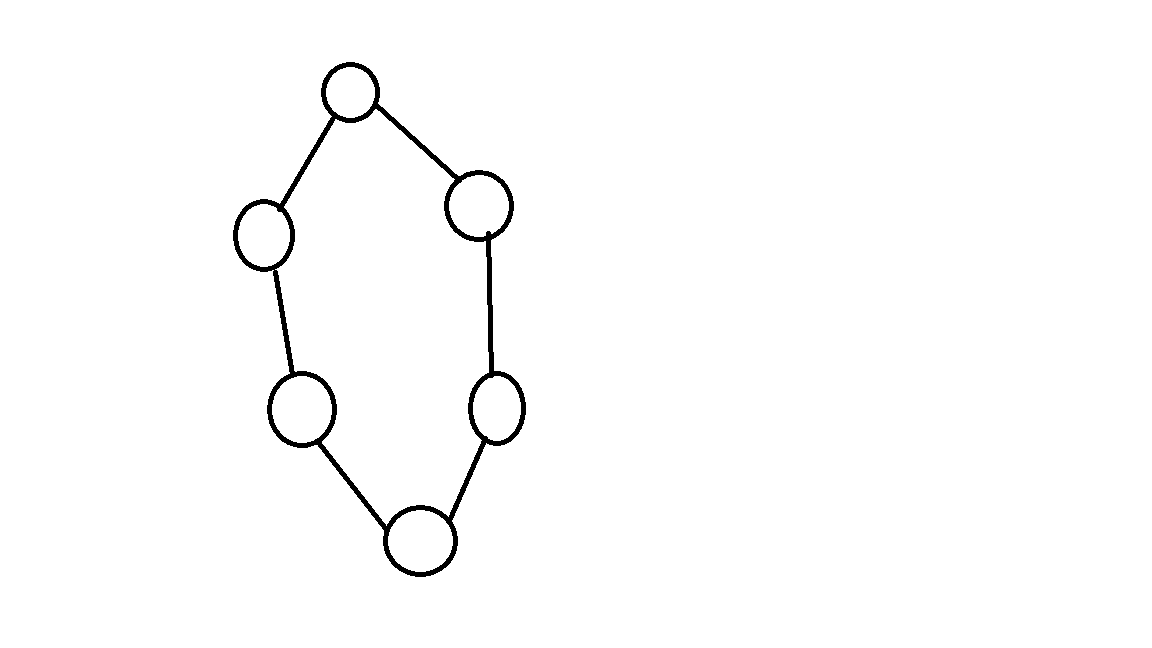
这种情况就会作为一个强连通分量被缩成一个点

在树上求两点之间的路径，边不能重复走，相当于求最近公共祖先

边权

在tarjan后面重新建图的部分需要遍历所有边，把一个强连通分量的边权直接作为点权加上，不同强联通分量的边权作为新建的边的边权，正反建两次，因为边不会重走，所以不会加重

lca预处理时dis[u][i]表示u到u的2ⁱ个祖先的路径中所有边权，点权的和，不包括u的2ⁱ个祖先的点权

dis[u][i]与fa处理思路类似，即dis[fa[u][i-1]][i-1]+dis[u][i-1]

因为dis不包括路径终点（祖宗）的点权，所以要找到lca后要把lca的点权加上

代码

#include<bits/stdc++.h>
using namespace std;
int cnt=0,head[600100],uu[600100],vv[600010],zz[600100],dfn[601000],low[600100],t=0,sum[600010],dis[600010][21],in[600010],dep[600100],fa[600010][21],color[600100],colornum=0,stac=0,sta[600010];
struct node{
	int w,nxt,to;
}road[600100];
void build(int u,int v,int z)
{
	road[++cnt].w=z;
	road[cnt].nxt=head[u];
	road[cnt].to=v;
	head[u]=cnt;
}
void tarjan(int f,int u)
{
	dfn[u]=low[u]=++t;
	in[u]=1,sta[++stac]=u;
	for(int i=head[u];i;i=road[i].nxt)
	{
		int v=road[i].to;
		if(v==f) continue;
		if(!dfn[v]) 
		{
			tarjan(u,v);
			low[u]=min(low[u],low[v]);
		}
		else if(in[v]) low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		color[u]=++colornum;
		in[u]=0;
		while(sta[stac]!=u)
		{
			color[sta[stac]]=colornum;
			in[sta[stac]]=0;
			stac--;
		}
		stac--;
	}
}
void dfs(int f,int u,int z)
{
	dep[u]=dep[f]+1;
	fa[u][0]=f;
	dis[u][0]=sum[u]+z;
	for(int i=1;i<=20;i++)
	{
		fa[u][i]=fa[fa[u][i-1]][i-1];
		dis[u][i]=dis[fa[u][i-1]][i-1]+dis[u][i-1];
	}
	for(int i=head[u];i;i=road[i].nxt)
	{
		int v=road[i].to;
		if(!dep[v]&&v!=f) dfs(u,v,road[i].w);
	}
}
int lca(int x,int y)
{
	int ans=0;
	if(dep[x]>dep[y]) swap(x,y);
	for(int i=20;i>=0;i--)
		if(dep[fa[y][i]]>=dep[x]) ans+=dis[y][i],y=fa[y][i];
	if(x==y) return ans+sum[x];//QAQ
	for(int i=20;i>=0;i--)
		if(fa[y][i]!=fa[x][i]) ans+=dis[x][i]+dis[y][i],x=fa[x][i],y=fa[y][i];
	if(fa[x][0]==fa[y][0]) return ans+sum[fa[x][0]]+dis[x][0]+dis[y][0];
	else return 0;
}
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>uu[i]>>vv[i]>>zz[i];
		build(uu[i],vv[i],zz[i]);
		build(vv[i],uu[i],zz[i]);
	}
	for(int i=1;i<=n;i++)
	{
		if(!dfn[i]) tarjan(0,i);
	}
	memset(head,0,sizeof(head));
	cnt=0;
	for(int i=1;i<=m;i++)
	{
		if(color[uu[i]]!=color[vv[i]])
		{
			build(color[uu[i]],color[vv[i]],zz[i]);
			build(color[vv[i]],color[uu[i]],zz[i]);
		}
		else sum[color[uu[i]]]+=zz[i];//缩点的时候如何处理边权 
	}
	for(int i=1;i<=colornum;i++)
	{
		if(!fa[i][0]) dfs(0,i,0);
	}
	int q,s,t;
	cin>>q;
	for(int i=1;i<=q;i++)
	{
		cin>>s>>t;
		int lcan=lca(color[s],color[t]);
		if(lcan>0) cout<<"YES"<<"
";
		else cout<<"NO"<<"
";
	}
	return 0;
 }