Lightning Conductor

如何把非细节题写成细节题

loj题目链接

洛谷题目链接

首先对于题目要求简单移项得到

p[i]>=a[j]-a[i]+sqrt(abs(i-j))

求p[i]的最小非负整数值

也就是求等号左边柿子的最大值

i是当前项，j是决策项，可以联想到dp

a[i]是定值

abs不好处理，可以转化成

对于j<=i求a[j]+sqrt(i-j)的最大值（等号？
​
对于j>i求a[j]+sqrt(j-i)的最大值

然后参考sqrt的函数图像（图源网络，侵删

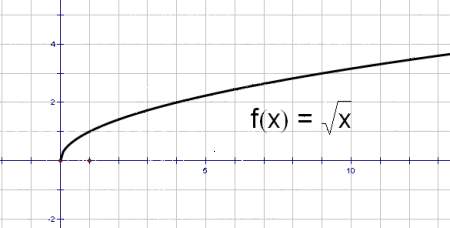
（没有函数图像的话自己带几个数进去试一试

那么把这个图像向右平移j，向上平移a[j]就可以得到a[j]+sqrt(i-j)

左右对称一下就是a[j]+sqrt(j-i)

原来的图像从原点开始，平移之后的图像会从j开始，

原来的图像向右延伸，对称之后向左延伸

对于很多决策点就是很多个如上图像

因为这些图像都是单增且增长速度也就是形状都一致

所以决策具有单调性（蒟蒻不会证明

我们要求在横坐标是i时的所有图像的纵坐标的最大值

因为增长速度的变慢的，

可以想像对于所有图像后出现的图像超过前一个成为决策点直到被后一个图像超过去

什么时候超过？也就是二分求一个函数图像的交点

如果前者的交点比后者出现的要晚（注意是晚而不一定是横坐标大

也就是它在超过前一个之前已经被后一个超过了

那么它就不会成为决策点可以直接扔掉

维护这样的一节一节的决策点（？

转移的时候只要再把被后面的超过的决策点扔掉剩下的第一个就是当前的决策点

#include<bits/stdc++.h>
using namespace std;
int a[600000],n,p[600000],line[600000];
int read()
{
	int x=0;
	char ch=getchar();
	while(ch<'0'||ch>'9') ch=getchar();
	while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
	return x;
}
double gety(int bx,int x)
{
	return a[bx]+sqrt((double)(bx-x));
}
int findpoi(int xi,int xj)//xi是后来的 
{
	int l=1,r=xi;
	if(gety(xi,0)<=gety(xj,0)) return 0;//特判没有交点的情况
	while(l<r)
	{
		int mid=(l+r)>>1;
		if(gety(xi,mid)>gety(xj,mid)) l=mid+1;//如果当前位置后来的已经超过新来的了，就要去先出现的位置找
                                                      //因为这里是倒序循环，所以横坐标大的先出现
		else r=mid;
	 } 
	 return l;
}
double gety_(int bx,int x)
{
	
	return a[bx]+sqrt((double)(x-bx));//如上
}
int findpoi_(int xi,int xj)//xj是后来的 
{
	int l=xj,r=n;
	if(gety_(xj,n+1)<=gety_(xi,n+1)) return n+1;//特判没有交点的情况
	while(l<r)
	{
		int mid=(l+r)>>1;
		if(gety_(xj,mid)<gety_(xi,mid)) l=mid+1;//如果后来的还没有超过，就去后出现的位置找
		else r=mid;
	 } 
	 
	 return l;
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++) a[i]=read();
	int head=1,tail=0;
	for(int i=n;i>=1;i--)
	{////////////////////line[tail]何时超过 line[tail-1]和line[tail]何时被i超过
		while(head<tail&&findpoi(line[tail],line[tail-1])<=findpoi(i,line[tail])) tail--;
		line[++tail]=i;
		/////////////////line[head]的巅峰时期已过已经被line[head+1]超过了 
		while(head<tail&&findpoi(line[head+1],line[head])>=i) head++;
		p[i]=max(p[i],(int)ceil(gety(line[head],i))-a[i]);//满足条件的最小非负整数 
	}
	head=1,tail=0;
	for(int i=1;i<=n;i++)
	{
		while(head<tail&&findpoi_(line[tail-1],line[tail])>=findpoi_(line[tail],i)) tail--;
		line[++tail]=i;
		while(head<tail&&findpoi_(line[head],line[head+1])<=i) head++;
		p[i]=max(p[i],(int)ceil(gety_(line[head],i))-a[i]);//满足条件的最小非负整数 
	}
	for(int i=1;i<=n;i++) cout<<p[i]<<"
";
	return 0;
}

int head=1,tail=0;
for(int i=n;i>=1;i--)
{
	while(head<tail&&findpoi(line[head+1],line[head])>=i) head++;
	if(head<=tail) p[i]=max(p[i],(int)ceil(gety(line[head],i))-a[i]);
        //决策点是本身的话答案就是0，0又是初始化的值，所以本身也可以不做决策点
        //但是需要特判一下没有入队，队为空的情况，直接做会拿0-i开方
	while(head<tail&&findpoi(line[tail],line[tail-1])<=findpoi(i,line[tail])) tail--;
	line[++tail]=i;
}

是不是太麻烦了，，，其实因为图像是对称一下，所以可以直接把a数组对称一下

#include<bits/stdc++.h>
using namespace std;
int a[600000],n,line[600000],p[600000];
double Poi[600000];
double val(int xi,int xj)
{
	return a[xj]+sqrt((double)abs(xi-xj));
}
int findpoi(int xi, int xj) 
{
    int l = xj, r = n + 1;
    while (l < r) 
    {
        int mid = (l + r) >> 1;
        if (val(mid, xj) < val(mid, xi)) l = mid + 1;
        else r = mid;
    }
    return l;
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	int h=1,t=0;
	for(int i=1;i<=n;++i){
    	while(h<t&&findpoi(line[t-1],line[t])>=findpoi(line[t],i))--t;
    	Poi[t]=findpoi(line[t],i),line[++t]=i;
    	while(h<t&&findpoi(line[h],line[h+1])<=i)++h;
    	p[i]=max(p[i],(int)ceil(val(i,line[h])));
    }
	h=1,t=0;
	for(int i=1;i<=n/2/*或者写成i<n-i+1*/;++i) swap(a[i],a[n-i+1]),swap(p[i],p[n-i+1]);
	//这样翻转一下
	for(int i=1;i<=n;++i){
    	while(h<t&&findpoi(line[t-1],line[t])>=findpoi(line[t],i))--t;
    	Poi[t]=findpoi(line[t],i),line[++t]=i;
    	while(h<t&&findpoi(line[h],line[h+1])<=i)++h;
    	p[i]=max(p[i],(int)ceil(val(i,line[h])));
    }
	for(int i=n;i;--i)printf("%d
",p[i]-a[i]);
	return 0;
}