一、树状数组基础
学OI的同学都知道,位运算(对二进制的运算)比普通运算快很多。同时我们接触到了状态压缩的思想(即将0-1的很多个状态压缩成十进制的一个数,每一个二进制位表示一个状态)。由于在实际做题过程当中,由于数据范围限制,我们必须采用更高效的存储、查询方法,于是树状数组应运而生。
首先我们检查传统的存储状态。对于数组的每一个下标i,其所存储的有效信息只有一个a[i](这是传统数组)。而对于树状数组,我们每一位下标可以存储lowbit(i)个有效信息。这个lowbit运算一会再说。所以尽管树状数组很难压缩真正的存储空间,但查询的时候可以把n的复杂度压缩成log(n)。这里的查询指区间查询和单点修改。
为什么有这样的查询效率?对于一个区间[1,x],我们把它分成log(x)个小区间。设x=2i1+2i2+……2im(这不由得让我们想起快速幂的分解方法),不妨设i1>i2>……>im,则我们可以把[1,x]分成以下小区间:
(1)长度为2i1的小区间[1,2i1]
(2)长度为2i2的小区间[2i1+1,2i1+2i2]
……
(log(n))长度为2im的小区间[2im-1+1,……+2im]
比如[1,6]可以分成[1,4]和[5,6]
所以我们如果想修改这个区间[1,x]的和,我们只需要修改这log(n)个区间的的和即可。
先上个图:
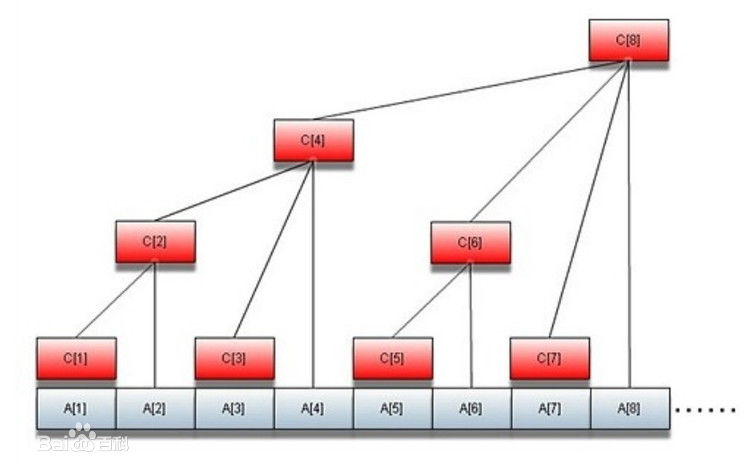
所以我们现在的问题在于,如果我们要查找a[idx]的前缀和,假设最开始idx是6:
则我们先加上最后一段小区间,令idx=6-21;
再加上第一段小区间,令idx=6-21-22。
应当注意的是,我们每次多减去的那个2i,实际上那个i是idx的二进制最靠近个位的那一位1对应到的数的编号。
举个例子:
10的二进制是1010,最靠近个位的一个1是在第二位,所以我们第一次减掉22;
得到的新数是8,二进制是1000,最靠近个位的一个1是在第四位,所以我们减掉24得到0。
我们减掉2k这个过程,我们把它量化,记原来的数组是a,我们开的数组是c,则每次我们加上的区间就是c[idx],然后idx往前移动到c[idx]存储的区间的前一位,继续这个步骤。
比如说,我们要计算a[1]到a[6]的和,我们让idx=6,我们发现刚才我们拆分[1,6]的结果最后一个小区间是[5,6],所以我们用c[6]记录a[5]+a[6],然后跳到c[4],用c[4]记录a[1]+a[2]+a[3]+a[4],即可得到答案。c数组就是我们说的树状数组。
那到底这个[1,n]的小区间怎么拆分?因为我们每次减掉的那个2i的i都是离个位最近的一个1所在的位置,所以我们只需要按照上述规则从后往前遍历n的所有二进制位,就可以遍历存储这个数的所有小区间。
比如说我们从6(110)遍历到4(100)(其中经过了[5,6]),然后遍历到0,其中经过了[1,4]。
也就是说,我们只需要找到每次要减掉的2i即可。
重点来了!!!
我们定义每次减掉的数是lowbit(i)(其中i是进行减法操作之前的数),也就是说lowbit(i)=2m,其中m是i的二进制最靠个位一个1的位置。定义了这个,我们实际上就是定义c[i]是以a[i]结尾长度为lowbit(i)的a数组内的区间,即c[i]=a[i-lowbit(i)+1]+a[i-lowbit(i)+2]+……+a[i]。这样每次idx跳跃一个lowbit(idx),就相当于恰好跳过了需要被加上的一段小区间,而加上这一段小区间的和只需要O(1)的复杂度。
怎么算这个lowbit(i)?这就要用到科学家们的智慧。
lowbit(i)=x&(-x)。
为什么这个数就能满足我们的要求?
我们来补充一点二进制的知识:
我们在存储一个数时,int类型是一个32位有符号整数,其中第一位是符号位,1表示负数,0表示正数。
这里利用的负数的存储特性,负数是以补码存储的,对于整数运算 x&(-x)有
● 当x为0时,即 0 & 0,结果为0;
●当x为奇数时,最后一个比特位为1,取反加1没有进位,故x和-x除最后一位外前面的位正好相反,按位与结果为0。结果为1。
●当x为偶数,且为2的m次方时,x的二进制表示中只有一位是1(从右往左的第m+1位),其右边有m位0,故x取反加1后,从右到左第有m个0,第m+1位及
其左边全是1。这样,x& (-x) 得到的就是x。
●当x为偶数,却不为2的m次方的形式时,可以写作x= y * (2^k)。其中,y的最低位为1。实际上就是把x用一个奇数左移k位来表示。这时,x的二进制表示最
右边有k个0,从右往左第k+1位为1。当对x取反时,最右边的k位0变成1,第k+1位变为0;再加1,最右边的k位就又变成了0,第k+1位因为进位的关系变成了1。
左边的位因为没有进位,正好和x原来对应的位上的值相反。二者按位与,得到:第k+1位上为1,左边右边都为0。结果为2^k。
总结一下:x&(-x),当x为0时结果为0;x为奇数时,结果为1;x为偶数时,结果为x中2的最大次方的因子。
一定注意,lowbit(0)会陷入死循环。
所以我们只需要利用这种运算,就可以在log(n)的复杂度内分割小区间,从而计算从a[1]到a[n]的和。
同样我们考虑修改一个值a[idx],因为c数组存储a数组的值有重复,所以我们必须将所有包含a[idx]的c[i]都进行修改。所以,同刚才的步骤,我们只需要根据某种顺序顺次查找每个包含a[idx]的c[i]即可。
这个顺序非常容易想到:
刚才我们已经知道,我们用c[i]表示从i往前数lowbit(i)个a[i]的总和。根据树状数组的特殊结构,我们查找的步骤如下:
找到c[i](肯定包含a[i])----->找到第一个包含c[i]的c[j]--------->找到第一个包含c[j]的c[k]……
一定注意这个步骤,这是因为树状数组的本质是一棵树,一个点只有一个父亲,这个我们之后会说。
根据lowbit的定义,同时根据二进制的特性,有以下两个特征:
(1)lowbit每向左移一位,其表示的lowbit(i)(也就是对应的区间长度,见前文)就乘以2;
(2)根据上文,我们要找到的数实际上是比他大的第一个lowbit往前移动一位的数(比如说5(101),6(110),lowbit移动了一位)。
所以我们怎么找这样的数???
要解决这个问题,我们必须回到二进制的加法:
比如说6+2,在二进制里的表示是这样的:
1 1 0
+0 1 0
---1-------
1 0 0 0
大家很容易注意到,第二位的两个1加起来之后进位到上一位一个1,因为上一位也有一个1,所以必须再进位;以此类推,它会一直进位直到进位到第一个数的lowbit前面的0上,把它变成1。
这难道不是我们刚才要的lowbit移动的方法??我们已经把最后一个1进位到了前面。我们只需要找到第二个和它相加的那个数即可。
因为要进位最后一个1,同时我们需要使底下那个数最小,所以我们只需要找到一个数,它前面后面都是0,中间那个与第一个数最后一个1对上的那一位是1.不明白的参见上面的例子。
有没有觉得上面这个很熟悉????
综上所述,我们得到:
(1)树状数组求前缀和:求1-i的和,每次加上c[i],然后减去lowbit(i)。
(2)树状数组单点修改:修改a[i]时修改c[idx],然后idx+=lowbit(idx),最开始idx=i。
二、树状数组的几何认识
刚才我们已经了解了树状数组的基本操作,下面我们从树本身的角度认识树状数组的性质和操作。
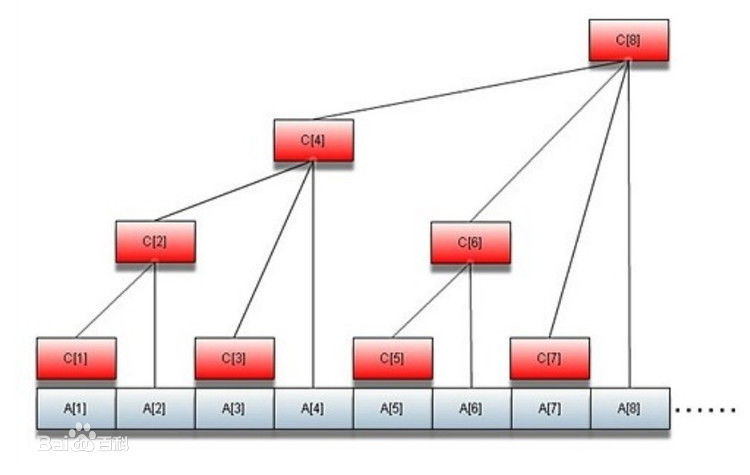
根据上面的图我们可以知道,树状数组具有以下几个性质:
(1)红色节点和其父亲之间的横向距离是lowbit(i),这是树状数组构建的基础,所以我们每次修改一个a[i]的值其实是修改所有以c[i]为根的且包含a[i]的子树的c[i]的值,也就是说从a[i]每次向上找到其父亲,并修改a[i]每一级父亲的值即可。
(2)查找一个点的前缀和时,相当于从这个点每次找到它的儿子覆盖的区间,而每个点覆盖的区间是从这个点到它最左边的儿子,所以每次减去lowbit(i)即可。
高级用法待填坑。