在大家都在为考试绞尽脑汁的时候,我这个无耻的人因为一个都不会而出来水两个题解整理一下这段时间学的Tarjan。
广东工业大学的题真是毒瘤,全是数学问题QAQ,我真是菜到死人 滚了滚了
那么我们首先来说一下这道题 。
。
这个难度真是令人愉快??????刚刚的不满全都烟消云散了呢?????过黑题脑残中。
题目背景
XS中学化学竞赛组教练是一个酷爱炉石的人。
有一天他一边搓炉石一边监考,而你作为一个信息竞赛的大神也来凑热闹。
然而你的化竞基友却向你求助了。
“第1354题怎么做”<--手语 他问道。
题目描述
你翻到那一题:给定一个烃,只含有单键(给初中生的一个理解性解释:就是一堆碳用横线连起来,横线都是单条的)。
然后炎魔之王拉格纳罗斯用他的火焰净化了一切环(???)。所有的环状碳都变成了一个碳。如图所示。
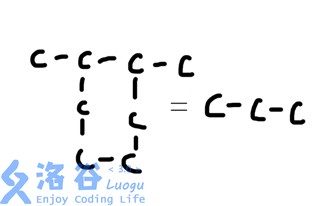
然后指定多组碳,求出它们之间总共有多少碳。如图所示(和上图没有关系)。

但是因为在考试,所以你只能把这个答案用手语告诉你的基友。你决定用二进制来表示最后的答案。如图所示(不要在意,和题目没有什么没关系)。
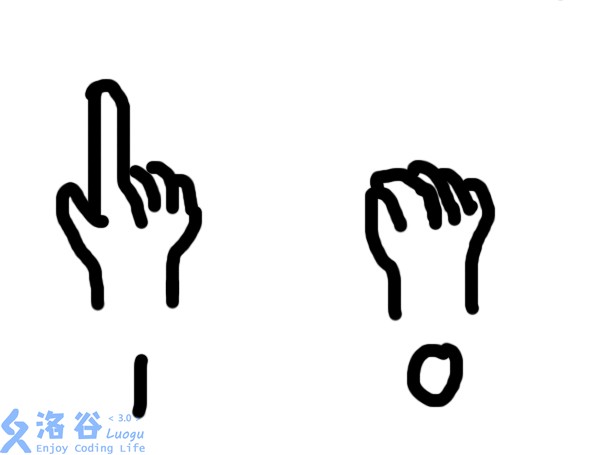 (这手势莫名诡异,第一次看到的时候看成了某些手势QAQ
(这手势莫名诡异,第一次看到的时候看成了某些手势QAQ
输入输出格式
输入格式:
第一行两个整数n,m.表示有n个点,m根键
接下来m行每行两个整数u,v表示u号碳和v号碳有一根键
接下来一个整数tot表示询问次数
接下来tot行每行两个整数,a,b表示询问的两个碳的编号
输出格式:
共tot行
每行一个二进制数
说明
1<n<=10000,1<m<=50000
(两个碳不成环)
Input
3 2 1 2 2 3 2 1 2 2 3
Output
3 2 1 2 2 3 2 1 2 2 3
祝大家AC愉快啦!!!
那么我们这题就结束了正式开始啦!
首先先说一下这题的基本题意: 给定一个无向图,其中一个点双联通分量算作一个点,询问两个点之间有多少点。
所以说这就是一道太监的祖先问题丫。显然.jpg
现在期待树剖的可以滚了 因为我不会
点双是什么??????这是个大问题【你以为这有个链接吗?实际上并没有!!
网上有很多这种讲解,这里就不细说了 毕竟这不是重点
所谓点-双连通分量是指在一个无向图中两点间至少有两条路径,且路径中(不算头尾)的点不同.
我们只要把所有的双联通分量缩成一个点,就可以得到一个新图。而
这个图又是一个连通图,所以说我们在缩点之后可以得到一个联通无环图 这不就是一颗小树苗?
询问两点之间有多点就是询问两个点的树上距离+1了啊
热动分析一下...........
我们会发现一点小小的问题...........
两个C是不成环的啊!!!
这完全违背了太监的能力啊!!!
基因型变异,即将变成秃头AA。
然而???.........
继续热动分析.............
死不放弃的精神一定会感动上天的!!
思路的花花迸溅:两个C不成环的话,我们在递归的时候只要不回到自己的爸爸就好了啊!!
这苟思路,浪费我5分钟。
热动分析结束。
这题居然有人跟我说:
“这道题,tarjan的时候最好用vector存边,不然第4个点死活过不去(不要问我为啥知道的),虽然我最后还是没用vector,但是链式前向星什么的,他死了。
不信的话你就尽情的尝试啊。”
很好你死了。我就不用vector你要咋(莫名耿气
当然,谨慎的你们还是vector吧,万一你的oj比较强呢??
下面放代码。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
#define MAXN 100010
using namespace std;
struct ss{
int next,to;
}dt[MAXN<<1];
int head[MAXN<<1],dept[MAXN],dfn[MAXN],low[MAXN];
int stk[MAXN],tu[MAXN],jump[MAXN][25],x[MAXN],y[MAXN];
int n,m,cnt,tag,top,num;
bool vis[MAXN];
inline int read() {
int sum=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9'){sum=(sum<<1)+(sum<<3)+ch-'0'; ch=getchar();}
return sum*f;
}//快读就完事了
inline void add(int u,int v) {
dt[++cnt].to=v;
dt[cnt].next=head[u];
head[u]=cnt;
return;
}
void tarjan(int now,int father) {
dfn[now]=low[now]=++tag;
stk[++top]=now;
vis[now]=true;
for(register int i=head[now];i;i=dt[i].next) {
int v=dt[i].to;
if(v==father) continue; //注意注意两c不成环
if(!dfn[v]) {
tarjan(v,now);
low[now]=min(low[now],low[v]);
}else if(vis[v])low[now]=min(low[now],low[v]);
}
if(dfn[now]==low[now]) {
++num;
while(int y=stk[top--]) {
tu[y]=num;
if(now==y) break;
}
}
}
void dfs(int now,int father) {
dept[now]=dept[father]+1;
jump[now][0]=father;
for(register int i=head[now];i;i=dt[i].next) {
int v=dt[i].to;
if(v!=father) dfs(v,now);
}
}
void RB() {
cnt=0;
memset(dt,0,sizeof(dt));
memset(head,0,sizeof(head));
for(register int i=1;i<=m;i++)
if(tu[x[i]]!=tu[y[i]]) {
add(tu[x[i]],tu[y[i]]);
add(tu[y[i]],tu[x[i]]);
}
return;
}
void Jump() {
for(register int i=1;i<=20;i++)
for(register int j=1;j<=cnt;j++)
jump[j][i]=jump[jump[j][i-1]][i-1];
return;
}
inline int LCA(int x,int y) {
if(x==y) return x;
if(dept[x]>dept[y]) swap(x,y);
for(register int i=20;i>=0;i--)
if(dept[jump[y][i]]>=dept[x]) y=jump[y][i];
if(x==y) return x;
for(register int i=20;i>=0;i--)
if(jump[x][i]!=jump[y][i]) {
x=jump[x][i];
y=jump[y][i];
}
return jump[x][0];
}
inline void putout(int now) {
int len=0;
int a[100]={0};//这个时候开在里面比较好
while(now) {
a[++len]=now%2;
now/=2;
}
for(register int i=len;i>=1;i--) printf("%d",a[i]);
cout<<endl;
}
void print(int q) {
while(q--) {
int x=read();
int y=read();
x=tu[x];
y=tu[y];
int lca=LCA(x,y);
int ans=dept[x]+dept[y]-(dept[lca]<<1)+1;
putout(ans);
}
return;
}
int main()
{
n=read();
m=read();
for(register int i=1;i<=m;i++) {
x[i]=read();
y[i]=read();
add(x[i],y[i]);
add(y[i],x[i]);
}
for(register int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i,0);
RB();
dfs(1,0);
Jump();
int q=read();
print(q);
return 0;
}
过黑题的感觉真棒!!
不过下次还是不要帮别人作弊了啊QAQ
谢谢!