题目描述
原题来自:AHOI 2012
暑假期间,小龙报名了一个模拟野外生存作战训练班来锻炼体魄,训练的第一个晚上,教官就给他们出了个难题。由于地上露营湿气重,必须选择在高处的树屋露营。小龙分配的树屋建立在一颗高度为 N+1N+1N+1 尺的大树上,正当他发愁怎么爬上去的时候,发现旁边堆满了一些空心四方钢材(如图 1.1),经过观察和测量,这些钢材截面的宽和高大小不一,但都是 111 尺的整数倍,教官命令队员们每人选取 NNN 个空心钢材来搭建一个总高度为 NNN 尺的阶梯来进入树屋,该阶梯每一步台阶的高度为 111 尺,宽度也为 111 尺。如果这些钢材有各种尺寸,且每种尺寸数量充足,那么小龙可以有多少种搭建方法?

注:为了避免夜里踏空,钢材空心的一面绝对不可以向上。
输入格式
一个正整数 NNN,表示阶梯的高度。
输出格式
一个正整数,表示搭建方法的个数。
注:搭建方法个数可能很大。
样例
样例输入 3
样例输出 5
样例说明
555 种搭建方法如下图:

数据范围与提示
对于全部数据,1≤N≤500。
背景
这是今天下午的t3。对我来说最简单的一道,也是唯一一道两遍AC的题目。
简直丢人,我居然一开始没看出来是高精度。。。QAQ
然后我就只写了个普通版的,发现WA掉之后才回来改的。
思路分析
其实这题还是不好看出来的。
首先递推关系是肯定能看出来的。
同机房某神犇教我怎么看,TA说:
看啊,样例输入3,输出5,这不就是卡特兰数嘛?多显然。
??????我*****的。
没看出来!
当然如果看出来就最好了【怎么可能???
没看出来也没问题,交给我吧。
开始分析:
首先,有图的题目一定要认真的观察图。
然后我们来仔细将这张图分解一下

这是一个4层的阶梯,我们把它分解一下。
这有很多种的构成方式,我们先尝试一下第一种。
第一种:
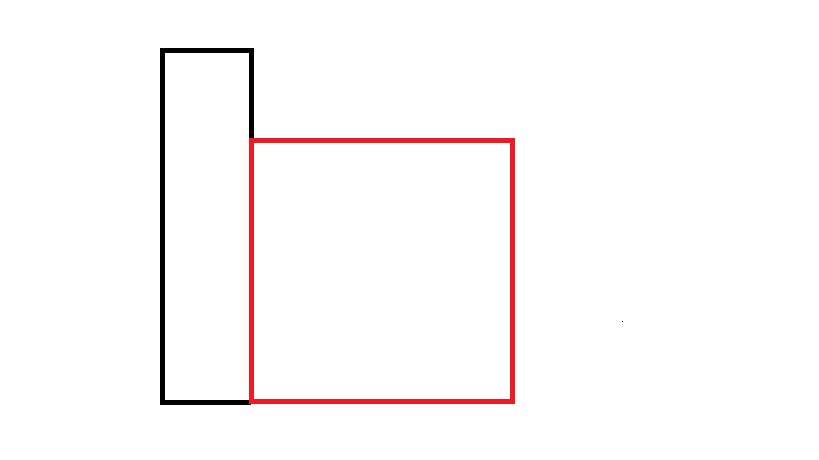
然后观察一下右边红色的部分,把它先拆掉。
方案一:
方案二:

方案..............
在这种构成方法下,我们能构成可行的树屋阶梯为 1 × 5 = 5 个。
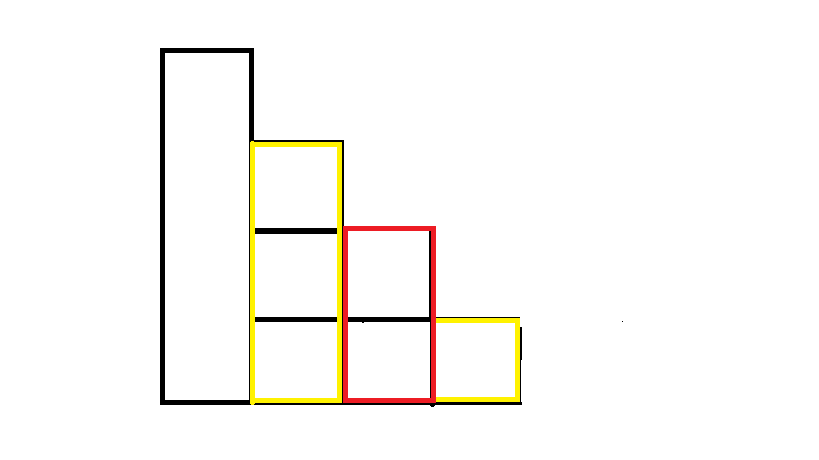
第二种:
方案一:

方案二:

等等等等。。。
这种构成方法下,我们能构成可行的树屋阶梯 1 × 2 = 2 个。
第n种:
。。。。。。
本质上是和上面的 2 种构成方法是一样的。所有方案数加在一起,得 f4 = 14
结论:
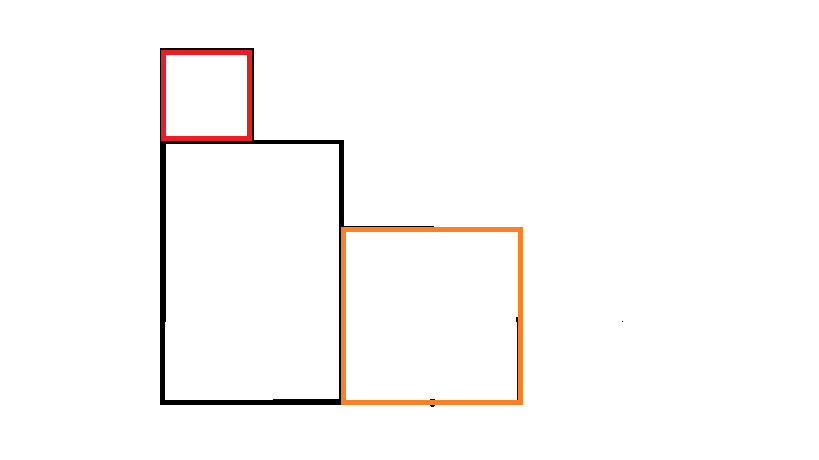
我们发现:对于任何大小的树屋阶梯,都可以由左上角放一块大小为 j 的以及右下角放一块大小为 i - j - 1 的树屋阶梯,再在空缺的地方由单个大块的矩形填充即可构成;
这个构成的树屋阶梯一共有 (j) + (i - j - 1) + 1个钢材,正好是 i 个。
因为 j 可以在 0 ~i - 1 取且可以证明每一个构成的树屋阶梯一定各不相同,所以我们可以得到树屋阶梯方案与大小关系的递推式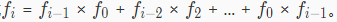
同时,我们规定 f0= f1 = 1。
来了来了,这不就是卡特兰数的递推式吗?
细节问题
?????一定要注意数据范围。
这题需要高精,原因是什么就不用说了吧。
那么这里介绍一种玄学,额似乎也不玄学的优化。


跑的贼快。
Python? 滚!
高精? 滚!
代码奉上
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> using namespace std; const int MA=120001; int n; int fz[MA],fm[MA]; int ans[MA*100],cnt;//ans最大整数的位数 int fpow(int x,int b) { int res=1; while(b) { if(b&1) res*=x; b>>=1; x*=x; } return res; } void mul(int x) { int k=0;//进位 for(int i=1;i<=cnt;i++) { ans[i]*=x; ans[i]+=k; k=ans[i]/10; ans[i]%=10; } while(k) { ans[++cnt]+=k; k=ans[cnt]/10; ans[cnt]%=10; } return; } int main() { scanf("%d",&n); for(int i=2;i<=n;i++) { int a=n+i; for(int j=2;j*j<=a;j++) {//从1开始没有意义 while(!(a%j)) { fz[j]++; a/=j; } } if(a>1) fz[a]++; int b=i; for(int j=2;j*j<=b;j++) {//从1开始没有意义 while(!(b%j)) { fm[j]++; b/=j; } } if(b>1) fm[b]++; } cnt=1; ans[0]=1; ans[1]=1;//卡特兰数 for(int i=2;i<=2*n;i++) { if(!fz[i]) continue; fz[i]-=fm[i]; if(!fz[i]) continue; int x=fpow(i,fz[i]); if(x!=1) mul(x); } for(int i=cnt;i>=1;i--) cout<<ans[i]; return 0; }