p1299如何三重循环A掉

　　先来渲染气氛.

　　

　　

　　我真的不知道怎么记忆化搜索,这里讲一下如何用几个循环A掉.

　　数对称的正方形是吧,我会n^5枚举!枚举顶点,枚举正方形长度,枚举其中的点判断是否合法.30分到手.100分需要n^3的算法.

---

 　　以下先考虑正方形长度为奇数的时候如何写.

---

　　考虑n^5如何向n^3转化?认真思考发现枚举中间的点好像有点蠢.能否想到预处理呢?我会预处理从一个点出发向下和哪个对称!这个方法存放较麻烦,最大空间需要n^3好吧也不算麻烦.复杂度应该是n^4,如何用n^3预处理?我会从一个点为中心向左右向上下枚举是否对称并更新到达的点的状态!(这里已经用到了动归的思想了).既然如此为何不预处理出从一个点为中心能构成对称的最大长度呢?这样判断的时候只需要看一下那个中点的最大长度是否大于等于需要的长度即可.n^5转化成了n^3+n^4,枚举中心,枚举长度,判断是否合法.

　　n^4还是有点大啊,考虑最后那个判断是否合法的n我们在干什么:对于长度k,判断 以中线上的点为中心向左右或向上下能构成的最大长度是否大于等于k.

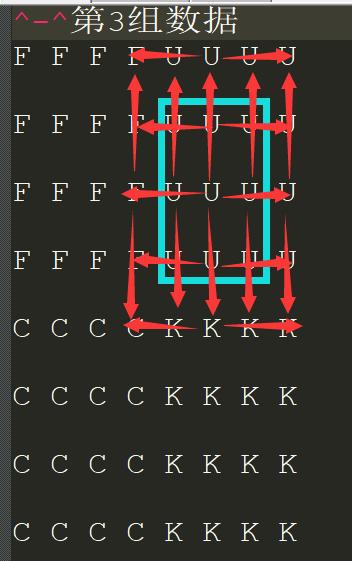
　　如果存在小于k的就break掉. 但是k-1长度的正方形的中先上的点已经遍历过了,如何利用之前的信息以达到O(1)判断的效果呢?再次利用动归的思想:我会记录min以中线上的点为中点的最长对称图形长度!利用它O(1)判断!好了你AC了.

n^3预处理出以每个点为中点最长的对称图形长度.
枚举中心点,每次向外拓展,利用新拓展的四个点的最长长度判断是否合法,并更新minn表示最短长度,如果k>minn就break,复杂度n^3

---

　　有了方法论,然后就是长度为偶数的如何处理了.我是所有的点都向左上偏一点.比如记录以每个点为中点向左偏一点的最长左右方向的对称图形长度这个样子.

　　写代码总不会比想思路更难了吧...

using namespace std;
int i,j,k,minn;
int shangxia[300][300],zuoyou[300][300];
char a[300][300],s[300];
int m,n,ans;
int main()
{
    cin>>m>>n;
    for(i=1;i<=m;i++)
    {
        cin>>s;
        for(j=1;j<=n;j++)
            a[i][j]=s[j-1];
    }
    for(i=1;i<=m;i++)
    {
        for(j=1;j<=n;j++)
        {
            k=1;
            while(i-k>0&&i+k<m+1)
                if(a[i-k][j]==a[i+k][j])
                    k++;
                else 
                    break;
            shangxia[i][j]=k-1;
            k=1;
            while(j-k>0&&j+k<n+1)
            {
                if(a[i][j-k]==a[i][j+k])
                    k++;
                else 
                    break;
            }
            zuoyou[i][j]=k-1;
        }
    }
    for(i=1;i<=m;i++)
    {
        for(j=1;j<=n;j++)
        {
            k=0;
            minn=min(zuoyou[i][j],shangxia[i][j]);
            while(i-k>0&&i+k<m+1&&j-k>0&&j+k<n+1)
            {
                ans++,k++;
                minn=min(zuoyou[i-k][j],minn);
                minn=min(zuoyou[i+k][j],minn);
                minn=min(shangxia[i][j-k],minn);
                minn=min(shangxia[i][j+k],minn);
                if(minn<k)break;
            }
        }
    }
        /*奇数*/
        //////////////////
        /*偶数*/
    memset(shangxia,0,sizeof(int));
    memset(zuoyou,0,sizeof(int));
    for(i=1;i<=m;i++)
    {
        for(j=1;j<=n;j++)
        {
            k=1;
            while(i-k+1>0&&i+k<m+1)
            {
                if(a[i-k+1][j]==a[i+k][j])
                    k++;
                else 
                    break;
            }
            shangxia[i][j]=k-1;
            k=1;
            while(j-k+1>0&&j+k<n+1)
            {
                if(a[i][j-k+1]==a[i][j+k])k++;
                else break;
            }
            zuoyou[i][j]=k-1;
        }
    }
    for(i=1;i<=m;i++)
    {
        for(j=1;j<=n;j++)
        {
            k=0;
            minn=min(zuoyou[i][j],shangxia[i][j]);
            while(i-k+1>0&&i+k<m+1&&j-k+1>0&&j+k<n+1)
            {
                k++;
                minn=min(zuoyou[i-k+1][j],minn);
                minn=min(zuoyou[i+k][j],minn);
                minn=min(shangxia[i][j-k+1],minn);
                minn=min(shangxia[i][j+k],minn);
                if(minn<k)break;
                ans++;
            }
        }
    }
    cout<<ans;
    return 0;
}