问题描述
跳跳棋是在一条数轴上进行的。棋子只能摆在整点上。每个点不能摆超过一个棋子。我们用跳跳棋来做一个简单的游戏:棋盘上有3颗棋子,分别在a,b,c这三个位置。我们要通过最少的跳动把他们的位置移动成x,y,z。(棋子是没有区别的)跳动的规则很简单,任意选一颗棋子,对一颗中轴棋子跳动。跳动后两颗棋子距离不变。一次只允许跳过1颗棋子。
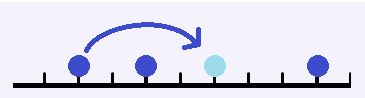
写一个程序,首先判断是否可以完成任务。如果可以,输出最少需要的跳动次数。
输入格式
第一行包含三个整数,表示当前棋子的位置a b c。(互不相同)
第二行包含三个整数,表示目标位置x y z。(互不相同)
输出格式
如果无解,输出一行NO。如果可以到达,第一行输出YES,第二行输出最少步数。
样例输入
1 2 3
0 3 5
样例输出
YES
2
数据范围
100% 绝对值不超过10^9
题解
中间的棋子可以往两边跳,两边最多只有一个能往中间跳
我们把初始状态的棋子从左到右编号,即最左边的棋子为1号,中间的棋子为2号,右边的棋子为3号【只是为了写题解方便(〃'▽'〃) 】
跳动前后两颗棋子距离不变,假设右边的棋子(即3号棋)可以往中间跳,那么跳完后,3号棋在中间,2号棋在右边,这时只要距离够大,2号棋可以以3号棋为中轴再往中间跳,跳完后只要距离够大,2号棋还可以再跳……
左边的棋子同理
起始状态可以往某个状态跳,目标状态也可以往某个状态跳,如果最终起始状态和目标状态可以跳到同一个状态,那么就存在一种方案可以从起始状态跳到目标状态。
这就有点像在二叉树上求两个节点的距离
求树上结点的距离用到最近公共祖先
有最近公共祖先就会有倍增
于是我们把所有状态表示成一棵二叉树,对于一个结点(即棋子的一种状态),两边的棋子往中间跳为其两个儿子,中间的棋子往两边跳为其父亲
问题转换为求树上两个结点的距离
可以构造这样的数据
1 2 1000000000
99999998 99999999 1000000000
这样左边要一直往中间跳上上亿次
我们发现若记前两个数差d1,后两个数差d2,不妨设d1<d2
则左边最多往中间跳(d2-1)/d1次
然后只能右边往中间跳,是一个辗转相除的过程,即在logK的时间内我们可以用这种方法得到某个结点向上跳K次后的结点,或者根节点,同时还可以顺便算下深度
那么只要求初始和目标的两个状态的深度d1,d2,将较深的调整到同一深度
然后二分/倍增求与lca的深度差x
ans=2*x+|d1-d2|
1 #include <cstdio> 2 struct node{ 3 int x,y,z; 4 }a,b; 5 int d[5],ans; 6 void Swap(int &x,int &y) 7 { 8 x^=y; y^=x; x^=y; 9 return; 10 } 11 node find(node s,int t,int p) 12 { 13 int i=0,j; 14 for (d[p]=0;t;d[p]+=i) 15 { 16 if (s.y-s.x>s.z-s.y) 17 { 18 j=s.z-s.y; 19 i=(s.y-s.x-1)/j; 20 if (i>t) i=t; 21 s.y-=i*j; s.z=s.y+j; 22 t-=i; 23 } 24 else if (s.y-s.x<s.z-s.y) 25 { 26 j=s.y-s.x; 27 i=(s.z-s.y-1)/j; 28 if (i>t) i=t; 29 s.y+=i*j; s.x=s.y-j; 30 t-=i; 31 } 32 else return s; 33 } 34 return s; 35 } 36 bool check(node a,node b) 37 { 38 return a.x==b.x && a.y==b.y && a.z==b.z; 39 } 40 int main() 41 { 42 int i,j,k; 43 node fa,fb,c; 44 scanf("%d%d%d",&a.x,&a.y,&a.z); 45 scanf("%d%d%d",&b.x,&b.y,&b.z); 46 if (a.x>a.y) Swap(a.x,a.y); 47 if (a.x>a.z) Swap(a.x,a.z); 48 if (a.y>a.z) Swap(a.y,a.z); 49 if (b.x>b.y) Swap(b.x,b.y); 50 if (b.x>b.z) Swap(b.x,b.z); 51 if (b.y>b.z) Swap(b.y,b.z); 52 fa=find(a,1e9,1); 53 fb=find(b,1e9,2); 54 if (!check(fa,fb)) 55 { 56 printf("NO "); 57 return 0; 58 } 59 printf("YES "); 60 if (d[1]>d[2]) 61 Swap(d[1],d[2]), 62 c=a,a=b,b=c; 63 b=find(b,d[2]-d[1],3); 64 int l=0,r=d[2],mid; 65 while (l<=r) 66 { 67 mid=(l+r)>>1; 68 if (check(find(a,mid,3),find(b,mid,3))) ans=mid,r=mid-1; 69 else l=mid+1; 70 } 71 printf("%d",ans*2+d[2]-d[1]); 72 return 0; 73 }