问题描述
花花有一棵带n个顶点的树T,每个节点有一个点权ai 。
有一天,他认为拥有两棵树更好一些。所以,他从T中删去了一条边。
第二天,他认为三棵树或许又更好一些。因此,他又从他拥有的某一棵树中去除了一条边。
如此往复。每一天,花花都会删去一条尚未被删去的边,直到他得到了一个包含了n棵只有一个点的树的森林。
定义一条简单路径的权值为路径上点权之和,一棵树的直径为树上权值最大的简单路径。花花认为树最重要的特征就是它的直径。所以他想请你算出任一时刻他拥有的所有树的直径的乘积。因为这个数可能很大,他要求你输出乘积对109+7取模之后的结果
输入格式

输出格式

样例输入

样例输出
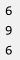
提示

数据范围

题解
把删边变成加边,倒过来做,维护直径,就变成了初始有n个集合,每个集合只有一个点,每次加一条边,合并两个集合,再求生成新树的直径
两棵树合并后的直径,它的端点一定从这两棵树原本的直径中取
预处理好最终树的形态,利用LCA和并查集
每次加边,更新直径的时候,要把答案除掉原来的直径的权值,而取模运算的规律对除法不适用,要用逆元转成乘法
1 #include <cstdio> 2 const int maxn=1e9+7; 3 struct node{ 4 int u,nex; 5 }g[200005]; 6 struct note{ 7 int u,v; 8 note(int u=0,int v=0):u(u),v(v){ } 9 }e[100005],p[100005]; 10 int n,a[100005],fir[100005],num,fa[100005],dep[100005],d[100005]; 11 int ans[100005],b[100005],dia[100005],f[100005][20],xx,yy,maxd; 12 void add(int x,int y) 13 { 14 g[++num].u=y; g[num].nex=fir[x]; fir[x]=num; 15 return; 16 } 17 int ksm(int a,int b) 18 { 19 int s=1; 20 while (b) 21 { 22 if (b&1) s=1ll*s*a%maxn; 23 a=1ll*a*a%maxn; 24 b>>=1; 25 } 26 return s; 27 } 28 int find(int x) 29 { 30 if (x==fa[x]) return x; 31 return fa[x]=find(fa[x]); 32 } 33 void dfs(int x,int fa) 34 { 35 int i,k; 36 dep[x]=dep[fa]+1; d[x]=d[fa]+a[x]; f[x][0]=fa; 37 for (i=1;i<=17;i++) 38 f[x][i]=f[f[x][i-1]][i-1]; 39 for (k=fir[x];k;k=g[k].nex) 40 if (g[k].u!=fa) 41 dfs(g[k].u,x); 42 return; 43 } 44 int lca(int x,int y) 45 { 46 int i; 47 if (dep[y]<dep[x]) x^=y,y^=x,x^=y; 48 for (i=17;i>=0;i--) 49 if (dep[f[y][i]]>=dep[x]) 50 y=f[y][i]; 51 if (x==y) return x; 52 for (i=17;i>=0;i--) 53 if (f[y][i]!=f[x][i]) 54 y=f[y][i],x=f[x][i]; 55 if (x==y) return x; 56 return f[x][0]; 57 } 58 void dis(int x,int y) 59 { 60 int par=lca(x,y),s; 61 s=d[x]+d[y]-d[par]*2+a[par]; 62 if (s>maxd) maxd=s,xx=x,yy=y; 63 return; 64 } 65 int main() 66 { 67 freopen("a.in","r",stdin); 68 int i,j,k,x,y,fu,fv; 69 scanf("%d",&n); 70 for (ans[n]=i=1;i<=n;i++) 71 scanf("%d",&a[i]), 72 ans[n]=1ll*ans[n]*a[i]%maxn, 73 dia[i]=a[i],fa[i]=i,p[i]=note(i,i); 74 for (i=1;i<n;i++) 75 scanf("%d%d",&x,&y), 76 add(x,y),add(y,x), 77 e[i]=note(x,y); 78 for (i=1;i<n;i++) 79 scanf("%d",&b[i]); 80 d[1]=a[1]; dfs(1,0); 81 for (i=n-1;i>=1;i--) 82 { 83 fu=find(e[b[i]].u); fv=find(e[b[i]].v); 84 ans[i]=1ll*ans[i+1]*ksm(dia[fu],maxn-2)%maxn*1ll*ksm(dia[fv],maxn-2)%maxn; 85 fa[fv]=fu; maxd=0; 86 dis(p[fu].u,p[fv].u); dis(p[fu].v,p[fv].v); 87 dis(p[fu].u,p[fv].v); dis(p[fu].v,p[fv].u); 88 if (dia[fu]>maxd) maxd=dia[fu],xx=p[fu].u,yy=p[fu].v; 89 if (dia[fv]>maxd) maxd=dia[fv],xx=p[fv].u,yy=p[fv].v; 90 dia[fu]=maxd; p[fu]=note(xx,yy); 91 ans[i]=1ll*ans[i]*maxd%maxn; 92 } 93 for (i=1;i<=n;i++) 94 printf("%d ",ans[i]); 95 return 0; 96 }