搬砖

问题描述

我不会告诉你 moreD 神犇最喜欢搬砖了。
砖，当然是指魔砖，魔法砖带有一个魔法标记，只能摆在区间[Li,Ri]里。
正所谓日久生情，moreD 对砖头的热爱已经到了一个忘我的境界，他认为砖头也是有生命的，他希望各个砖可以和睦相处。具体来说是砖头越多越好。
moreD 每一次选定一个区间，然后选定一些砖头放入。使得这些砖头互不重叠，且任意选定的砖头的魔法标记不超出 moreD 选定的区间。
对于 moreD 每一次选定的区间，你需要回答 moreD，他最多可放入多少砖头哦。

输入格式

输出格式

样例输入

样例输出

数据范围

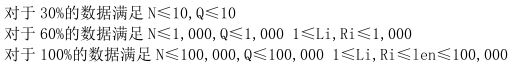
题解

f[i,j]表示从位置 i 开始，选择 2^j块砖，Ri 最大的线段 Ri 最小是多少。

f[i][j]= f[f[i][j-1]+1][j-1]

由样例可以发现一块砖的右端点和另一块砖的左端点相同也算重叠，所以这里f[i][j-1]要+1

询问时,对于区间[x,y]我们从 x 开始，从大到小枚举 k，如果选择 2^k 块砖后没有超出区间的范围，那么答案加上 2^k，然后继续统计 f[x,k]+1_~y 这段区间的答案。这样单次询问复杂度是 O(logn)的，询问的总复杂度是 O(Qlogn)，可以解决这道题。

#include <algorithm>
#include <cstdio>
struct node{
    int st,ed;
}a[100005];
int n,Q,len,ans,f[100005][20];
bool cmp(node x,node y)
{
    return x.st<y.st;
}
int min(int x,int y)
{
    return x<y?x:y;
}
int main()
{
    int i,j,x,y,l,r,t;
    scanf("%d%d%d",&n,&Q,&len);
    for (i=1;i<=n;i++) 
      scanf("%d%d",&x,&y),
      a[i].st=x,a[i].ed=y;
    std::sort(a+1,a+n+1,cmp);
    f[len+1][0]=len+1;  r=len+1;  t=n;
    for (i=len;i>=1;i--)
    {
        while (a[t].st==i && t>=1)
          r=min(r,a[t].ed),t--;
        f[i][0]=r;
    }
    for (j=1;j<=17;j++)
      for (i=1;i<=len;i++)
        f[i][j]=(f[i][j-1]==len+1?len+1:f[f[i][j-1]+1][j-1]);
    
    while (Q--)
    {
        scanf("%d%d",&l,&r);
        ans=0;
        for (i=17;i>=0;i--)
          if (f[l][i]<=r)
            ans|=(1<<i),
            l=f[l][i]+1;
        printf("%d
",ans);
    }
    return 0;
}