转自:http://www.cnblogs.com/dwdxdy/p/3261742.html
一、问题描述
问题描述:N个人分配N项任务,一个人只能分配一项任务,一项任务只能分配给一个人,将一项任务分配给一个人是需要支付报酬,如何分配任务,保证支付的报酬总数最小。
问题数学描述:

二、实例分析---穷举法
在讲将匈牙利算法解决任务问题之前,先分析几个具体实例。
以3个工作人员和3项任务为实例,下图为薪酬图表和根据薪酬图表所得的cost矩阵。

利用最简单的方法(穷举法)进行求解,计算出所有分配情况的总薪酬开销,然后求最小值。
total_cost1 = 250 + 600 + 250 = 1100; x00 = 1,x11 = 1,x22 = 1;
total_cost2 = 250 + 350 + 400 = 1000; x00 = 1,x12 = 1,x21 = 1;
total_cost3 = 400 + 400 + 250 = 1050; x01 = 1,x10 = 1,x22 = 1;
total_cost4 = 400 + 350 + 200 = 950; x01 = 1,x12 = 1,x20 = 1; //最优分配
total_cost5 = 350 + 400 + 400 = 1150; x02 = 1,x10 = 1,x21 = 1;
total_cost6 = 350 + 600 + 250 = 1150; x02 = 1,x11 = 1,x22 = 1;
对于任务数和人员数较少时,可利用穷举法计算结果。
若将N任务分配给N个人员,其包含的所有分配情况数目为N!,N增大时,穷举法将难以完成任务。
三、匈牙利算法
下面简要介绍匈牙利算法。
其基本的理论基础是针对cost矩阵,将cost矩阵的一行或一列数据加上或减去一个数,其最优任务分配求解问题不变。

算法的基本步骤如下:

四、实例分析---匈牙利算法
下面结合具体实例,分析匈牙利算法如何解决任务分配问题。
以N = 4为实例,下图为cost列表和cost矩阵。

Step1.从第1行减去75,第2行减去35,第3行减去90,第4行减去45。
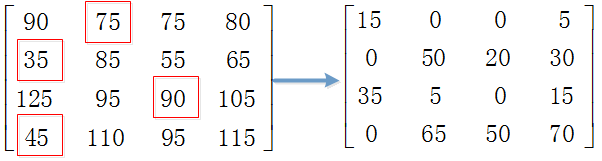
Step2.从第1列减去0,第2列减去0,第3列减去0,第4列减去5。
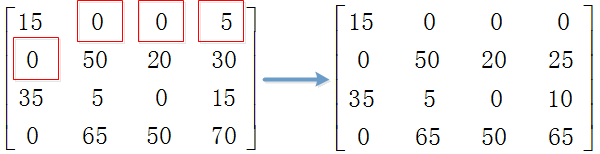
Step3.利用最少的水平线或垂直线覆盖所有的0。
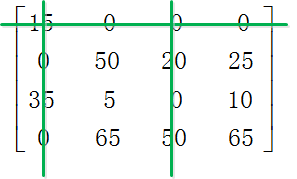
Step4.由于水平线和垂直线的总数是3,少于4,进入Step5。
Step5.没有被覆盖的最小值是5,没有被覆盖的每行减去最小值5,被覆盖的每列加上最小值5,然后跳转到步骤3.

Step3.利用最少的水平线或垂直线覆盖所有的0。

Step4.由于水平线和垂直线的总数是3,少于4,进入Step5。
Step5.没有被覆盖的最小值是20,没有被覆盖的每行减去最小值20,被覆盖的每列加上最小值20,然后跳转到步骤3.

Step3.利用最少的水平线或垂直线覆盖所有的0。
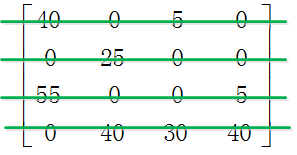
Step4.由于水平线和垂直线的总数是4,算法结束,分配结果如下图所示。

其中,黄色框表示分配结果,左边矩阵的最优分配等价于左边矩阵的最优分配。