poj2722

题意：给出若干个正方形的边长，和平面直角坐标系中的两条起点在原点的射线（射线上的点表示射线），两条射线在第一象限。要求用这些正方形和这两条射线围成一块封闭的面积，求最大面积。

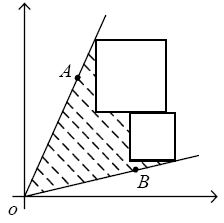
分析：把正方形对角线连成一条直线，排成一个斜率为-1的直线。这样才能保证面积最大。

所以现在的问题变为，已知两条射线的方向，以及三角形第三条边的斜率（斜率为-1）和长度（正方形边长和×sqrt（2））求三角形的面积（当然最终结果是三角形面积减去正方形面积的一半）

设有a，b两向量，方向是两射线方向，设ka*a为三角形的一条射线上的边，kb×b为三角形另一条射线上的边。（即将两向量适当延长）

延长后两向量的差即为第三条边的向量，由于第三条边斜率为-1,所以其对应向量的横纵坐标相等。且均等于正方形边长之和，设边长之和为a

可得方程：ka * xa - kb * xb = kb * yb - ka * ya = a

我们要求的三角形面积用叉积方法表示为：ka * xa * kb * yb - kb * xb * ka * xa

整理可得最终三角形面积为：a * a * (xa + ya) * (xb + yb) / (xa * yb - xb * ya)

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
usingnamespace std;

int n;

void swap1(double&a, double&b)
{
    double t = a;
    a = b;
    b = t;
}

int main()
{
    //freopen("t.txt", "r", stdin);
while (scanf("%d", &n), n)
    {
        double xa, ya, xb, yb;
        double a =0, s =0;
        scanf("%lf%lf%lf%lf", &xa, &ya, &xb, &yb);
        if (ya / xa > yb / xb)
        {
            swap1(ya, yb);
            swap1(xa, xb);
        }
        for (int i =0; i < n; i++)
        {
            double x;
            scanf("%lf", &x);
            a += x;
            s += x * x;
        }
        double ans = ((xa + ya) * a * (xb + yb) / (xa * yb - xb * ya) * a - s) /2;
        printf("%.3f\n", (double)ans);
    }
    return0;
}