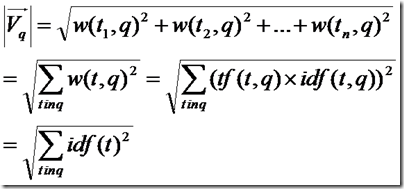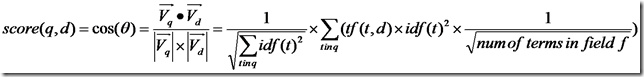Solr In Action 笔记(2) 之 评分机制(相似性计算)

Solr In Action 笔记(2) 之评分机制(相似性计算)

1 简述

     我们对搜索引擎进行查询时候，很少会有人进行翻页操作。这就要求我们对索引的内容提取具有高度的匹配性，这就搜索引擎文档的相似性计算，如何准确的选出最符合查询条件的文档。

     《这就是搜索引擎》里面对相似性计算进行了简单的介绍。

      内容的相似性计算由搜索引擎的检索模型建模，它是搜索引擎的理论基础，为量化相关性提供了一种数学模型，否则没法计算。当然检索模型理论研究存在理想化的隐含假设，即假设用户需求已经通过查询非常清晰明确地表达出来了，所以检索模型的任务不牵扯到对用户需求建模，但实际上这个和实际相差较远，即使相同的查询词，不同用户的需求目的可能差异很大，而检索模型对此无能为力。几种常见的检索模型有：

• 布尔模型：数学基础是集合论，文档和用户查询由其包含的单词集合来表示，两者的相似性则通过布尔代数运算来进行判定；缺点是其结果输出是二元的（相关和不相关），无法得出多大程度相关的结果，也就无法排序，同时让用户以布尔表达式进行搜索要求过高；
• 向量空间模型：把文档看成是由t维特征组成的一个向量，特征一般采用单词，每个特征会根据一定依据计算其权重，这t维带有权重的特征共同构成了一个文档，以此来表示文档的主题内容。计算文档的相似性可以采用Cosine计算定义，实际上是求文档在t维空间中查询词向量和文档向量的夹角，越小越相似；对于特征权重，可以采用Tf*IDF框架，Tf是词频，IDF是逆文档频率因子指的是同一个单词在文档集合范围的出现次数，这个是一种全局因子，其考虑的不是文档本身的特征，而是特征单词之间的相对重要性，特征词出现在其中的文档数目越多，IDF值越低，这个词区分不同文档的能力就越差，这个框架一般把Weight=Tf*IDF作为权重计算公式，当然向量空间的缺点是其是个经验模型，是靠直觉和经验不断摸索和完善的，缺乏一个明确的理论来引导其改进方向，例如求Tf和IDF值的时候为了惩罚长文档，都需要加入经验值；
• 概率模型：是目前效果最好的模型之一，okapi BM25这一经典概率模型计算公式已经在商业搜索引擎的网页排序中广泛使用。概率检索模型是从概率排序原理推导出来的，其基本思想是：给定一个用户查询，如果搜索系统能够在搜索结果排序时按照文档和用户需求的相关性由高到底排序，那么这个搜索系统的准确性是最优的。在文档集合的基础上尽可能准确地对这种相关性进行估计就是其核心。
• 语言模型：1998年首次提出，其他的检索模型的思考路径是从查询到文档，即给定用户查询，如何找出相关的文档，该模型的思路正好想法，是由文档到查询这个方向，即为每个文档建立不同的语言模型，判断由文档生成用户查询的可能性有多大，然后按照这种生成概率由高到低排序，作为搜索结果。语言模型代表了单词或者单词序列在文档中的分布情况；
• 机器学习排序算法：随着搜索引擎的发展，对于某个网页进行排序需要考虑的因素越来越多，这是无法根据人工经验完成的，这时候用机器学习就是非常合适的，例如Google目前的网页排序公式考虑了200多种因子。机器学习需要的数据源在搜索引擎中较好满足，例如用户的搜索点击记录。其分成人工标注训练、文档特征抽取、学习分类函数以及在实际搜索系统中采用机器学习模型等4个步骤组成。人工标注训练可由用户点击记录来模拟人为对文档相关打分的机制。

2 向量空间模型

    简述中介绍了好多种相似性计算方法，Solr采用了最基本的向量空间模型，本节就主要介绍下向量空间模型。其他的向量空间模型以后有时间进行学习吧。

    Solr的索引文件中有.tvx,.tvd,tvf存储了term vector的信息，首先我们学习如何利用term vector来反映相似性程度。

    用v(d1)表示了term d1的term向量，向量空间模型中，两个term的相似程度是计算向量空间坐标系中两个term向量的夹角，如果夹角越小，说明相似程度越大，而角度的计算可以使用余弦定理计算。

    给定一个查询以及一个文档，如何计算他们的相似值呢，请看以下公式，它使用了以下概念：term frequency (tf), inverse document frequency (idf), term boosts (t.getBoost), field normalization (norm), coordination factor (coord), and query normalization (queryNorm). 

•  t = term, d = document, q = query , f = field
•  tf(t in d ) 表示该term 在 这个文档里出现的频率(即出现了几次)。
•  idf(t) 表示 出现该term的文档个数。
•  t.getBoost() 查询语句中每个词的权重，可以在查询中设定某个词更加重要。
 norm(t,d) 标准化因子d.getBoost() • lengthNorm(f) • f.getBoost() ，它包括三个参数：
• Document boost：此值越大，说明此文档越重要。
• Field boost：此域越大，说明此域越重要。
• lengthNorm(field) = (1.0 / Math.sqrt(numTerms))：一个域中包含的Term总数越多，也即文档越长，此值越小，文档越短，此值越大。
• coord(q,d)：一次搜索可能包含多个搜索词，而一篇文档中也可能包含多个搜索词，此项表示，当一篇文档中包含的搜索词越多，则此文档则打分越高 ,numTermsInDocumentFromQuery / numTermsInQuery 
• queryNorm(q)：计算每个查询条目的方差和，此值并不影响排序，而仅仅使得不同的query之间的分数可以比较。

3 评分机制

• tf, 表示term匹配文章的程度，如果在一篇文章中该term出现了次数越多，说明该term对该文章的重要性越大，因而更加匹配。相反的出现越少说明该term越不匹配文章。但是这里需要注意，出现次数与重要性并不是成正比的，比如term A出现10次，term B出现1次，对于该文章的重要性term A并不是term B的10倍，所以这里tf的值进行平方根计算。

tf(t in d) = numTermOccurrencesInDocument ^1/2

• idf, 表示包含该文章的个数，与tf不同，idf 越大表明该term越不重要。比如this很多文章都包含，但是它对于匹配文章帮助不大。这也如我们程序员所学的技术，对于程序员本身来说，这项技术掌握越深越好（掌握越深说明花时间看的越多，tf越大），找工作时越有竞争力。然而对于所有程序员来说，这项技术懂得的人越少越好（懂得的人少df小），找工作越有竞争力。人的价值在于不可替代性就是这个道理。

idf(t) = 1 + log (numDocs / (docFreq +1)) 

• t.getBoost，boost是人为给term提升权重的过程，我们可以在Index和Query中分别加入term boost，但是由于Query过程比较灵活，所以这里介绍给Query boost。term boost 不仅可以对Pharse进行，也可以对单个term进行，在查询的时候用^后面加数字表示：
  • title:(solr in action)^2.5  对solr in action 这个pharse设置boost
  • title:(solr in action)  默认的boost时1.0
  • title:(solr^2in^.01action^1.5)^3OR"solrinaction"^2.5 
• norm(t,d) 即field norm，它包含Document boost，Field boost，lengthNorm。相比于t.getBoost()可以在查询的时候进行动态的设置，norm里面的f.getBoost()和d.getBoost()只能建索引过程中设置，如果需要对这两个boost进行修改，那么只能重建索引。他们的值是存储在.nrm文件中。

norm(t,d) = d.getBoost() • lengthNorm(f) • f.getBoost() 

• • d.getBoost() document的boost，对document设置boost是通过对每一个field设置boost实现的。
  • f .getBoost() field的boost，这里需要提以下，Solr是支持多值域方式建索引的，即同一个field多个value，如以下代码。当一个文档里出现同名的多值域时候，倒排索引和项向量都会在逻辑上将这些域的词汇单元附加进去。当对多值域进行存储的时候，它们在文档中的存储顺序是分离的，因此当你在搜索期间对文档进行检索时，你会发现多个Field实例。如下图例子所示，当查询author：Lucene时候出现两个author域，这就是所谓的多值域现象。

  • 1 Document doc = new Document();
    2 for (String author : authors){
    3     doc.add(new Field("author",author,Field.Store.YES,Field.Index.ANALYZED));
    4 }

    //首先对多值域建立索引
    Directory dir = FSDirectory.open(new File("/Users/rcf/workspace/java/solr/Lucene"));
    IndexWriterConfig indexWriterConfig = new IndexWriterConfig(Version.LUCENE_48,new WhitespaceAnalyzer(Version.LUCENE_48));
    @SuppressWarnings("resource")
    IndexWriter writer = new IndexWriter(dir,indexWriterConfig);
    Document doc = new Document();
    doc.add(new Field("author","lucene",Field.Store.YES,Field.Index.ANALYZED));
    doc.add(new Field("author","solr",Field.Store.YES,Field.Index.ANALYZED));
    doc.add(new Field("text","helloworld",Field.Store.YES,Field.Index.ANALYZED));
    writer.addDocument(doc);
    writer.commit();
    //对多值域进行查询
    IndexReader reader = IndexReader.open(dir);
    IndexSearcher search = new IndexSearcher(reader);
    Query query = new TermQuery(new Term("author","lucene"));
    TopDocs docs = search.search(query, 1);
    Document doc = search.doc(docs.scoreDocs[0].doc);
    for(IndexableField field : doc.getFields()){
        System.out.println(field.name()+":"+field.stringValue());
    }
    System.out.print(docs.totalHits);
    //运行结果
    author:lucene
    author:solr
    text:helloworld
    2

    当对多值域设置boost的时候，那么该field的boost最后怎么算呢？即为每一个值域的boost相乘。比如title这个field，第一次boost是3.0，第二次1，第三次0.5,那么结果就是3*1*0.5.

    • Boost: (3) · (1) · (0.5) = 1.5

• • lengthNorm, Norm的长度是field中term的个数的平方根的倒数，field的term的个数被定义为field的长度。field长度越大，Norm Field越小，说明term越不重要，反之越重要，这很好理解，在10个词的title中出现北京一次和在有200个词的正文中出现北京2次，哪个field更加匹配，当然是title。
  • 最后再说明下，document boost，field boost 以及lengthNorm在存储为索引是以byte形式的，编解码过程中会使得数值损失，该损失对相似值计算的影响微乎其微。
• queryNorm,  计算每个查询条目的方差和，此值并不影响排序，而仅仅使得不同的query之间的分数可以比较。也就说，对于同一词查询，他对所有的document的影响是一样的，所以不影响查询的结果，它主要是为了区分不同query了。

queryNorm(q) = 1 / (sumOfSquaredWeights )

sumOfSquaredWeights = q.getBoost()² • ∑ ( idf(t) • t.getBoost() )² 

coord(q,d)，表示文档中符合查询的term的个数，如果在文档中查询的term个数越多，那么这个文档的score就会更高。

numTermsInDocumentFromQuery / numTermsInQuery 

        比如Query：AccountantAND("SanFrancisco"OR"NewYork"OR"Paris") 

        文档A包含了上面的3个term，那么coord就是3/4，如果包含了1个，则coord就是4/4

4 源码

    上面介绍了相似值计算的公式，那么现在就来查看Solr实现的代码，这部分实现是在DefaultSimilarity类中。

  @Override
  public float coord(int overlap, int maxOverlap) {
    return overlap / (float)maxOverlap;
  }

  @Override
  public float queryNorm(float sumOfSquaredWeights) {
    return (float)(1.0 / Math.sqrt(sumOfSquaredWeights));
  }

  @Override
  public float lengthNorm(FieldInvertState state) {
    final int numTerms;
    if (discountOverlaps)
      numTerms = state.getLength() - state.getNumOverlap();
    else
      numTerms = state.getLength();
   return state.getBoost() * ((float) (1.0 / Math.sqrt(numTerms)));
  }

  @Override
  public float tf(float freq) {
    return (float)Math.sqrt(freq);
  }

  @Override
  public float idf(long docFreq, long numDocs) {
    return (float)(Math.log(numDocs/(double)(docFreq+1)) + 1.0);
  }

Solr计算score(q,d)的过程如下：

1:调用IndexSearcher.createNormalizedWeight()计算queryNorm()；

 1   public Weight createNormalizedWeight(Query query) throws IOException {
 2     query = rewrite(query);
 3     Weight weight = query.createWeight(this);
 4     float v = weight.getValueForNormalization();
 5     float norm = getSimilarity().queryNorm(v);
 6     if (Float.isInfinite(norm) || Float.isNaN(norm)) {
 7       norm = 1.0f;
 8     }
 9     weight.normalize(norm, 1.0f);
10     return weight;
11   }

具体实现步骤如下：

• Weight weight = query.createWeight(this);

• • 创建BooleanWeight->new TermWeight()->this.stats = similarity.computeWeight)->this.weight = idf * t.getBoost()

  •     public IDFStats(String field, Explanation idf, float queryBoost) {
          // TODO: Validate?
          this.field = field;
          this.idf = idf;
          this.queryBoost = queryBoost;
          this.queryWeight = idf.getValue() * queryBoost; // compute query weight
        }

• 计算sumOfSquaredWeights

• s = weights.get(i).getValueForNormalization()计算( idf(t) • t.getBoost() )² 如以下代码所示，queryWeight在上一部中计算出

•     public float getValueForNormalization() {
        // TODO: (sorta LUCENE-1907) make non-static class and expose this squaring via a nice method to subclasses?
        return queryWeight * queryWeight;  // sum of squared weights
      }

• • BooleanWeight->getValueForNormalization->sum = (q.getBoost)² *∑(this.weight)² = (q.getBoost)² *∑(idf * t.getBoost())²

• •  1     public float getValueForNormalization() throws IOException {
     2       float sum = 0.0f;
     3       for (int i = 0 ; i < weights.size(); i++) {
     4         // call sumOfSquaredWeights for all clauses in case of side effects
     5         float s = weights.get(i).getValueForNormalization();         // sum sub weights
     6         if (!clauses.get(i).isProhibited()) {
     7           // only add to sum for non-prohibited clauses
     8           sum += s;
     9         }
    10       }
    11 
    12       sum *= getBoost() * getBoost();             // boost each sub-weight
    13 
    14       return sum ;
    15     }

• 计算完整的querynorm() = 1 / Math.sqrt(sumOfSquaredWeights));

• 1   public float queryNorm(float sumOfSquaredWeights) {
  2     return (float)(1.0 / Math.sqrt(sumOfSquaredWeights));
  3   }

• weight.normalize(norm, 1.0f) 计算norm()

• topLevelBoost *= getBoost();   

• 计算value = idf()*queryWeight*queryNorm=idf()²*t.getBoost()*queryNorm（queryWeight在前面已计算出）

•     public void normalize(float queryNorm, float topLevelBoost) {
        this.queryNorm = queryNorm * topLevelBoost;
        queryWeight *= this.queryNorm;              // normalize query weight
        value = queryWeight * idf.getValue();         // idf for document
      }

2：调用IndexSearch.weight.bulkScorer()计算coord(q,d),并获取每一个term的docFreq，并将docFreq按td从小到大排序。

if (optional.size() == 0 && prohibited.size() == 0) {
        float coord = disableCoord ? 1.0f : coord(required.size(), maxCoord);
        return new ConjunctionScorer(this, required.toArray(new Scorer[required.size()]), coord);
      }

3：score.score()进行评分计算,获取相似值，并放入优先级队列中获取评分最高的doc id。

• weightValue= value =idf()²*t.getBoost()*queryNorm
• sore = ∑(tf()*weightValue)*cood 计算出最终的相似值
• 这里貌似没有用到lengthNorm，

    public float score(int doc, float freq) {
      final float raw = tf(freq) * weightValue; // compute tf(f)*weight
      
      return norms == null ? raw : raw * decodeNormValue(norms.get(doc));  // normalize for field
    }

  public float score() throws IOException {
    // TODO: sum into a double and cast to float if we ever send required clauses to BS1
    float sum = 0.0f;
    for (DocsAndFreqs docs : docsAndFreqs) {
      sum += docs.scorer.score();
    }
    return sum * coord;
  }

public void collect(int doc) throws IOException {
      float score = scorer.score();

      // This collector cannot handle these scores:
      assert score != Float.NEGATIVE_INFINITY;
      assert !Float.isNaN(score);

      totalHits++;
      if (score <= pqTop.score) {
        // Since docs are returned in-order (i.e., increasing doc Id), a document
        // with equal score to pqTop.score cannot compete since HitQueue favors
        // documents with lower doc Ids. Therefore reject those docs too.
        return;
      }
      pqTop.doc = doc + docBase;
      pqTop.score = score;
      pqTop = pq.updateTop();
    }

5 公式推导

    关于公式的推导觉先的《Lucene学习总结之六：Lucene打分公式的数学推导》可以查看这部分内容。

我们把文档看作一系列词(Term)，每一个词(Term)都有一个权重(Term weight)，不同的词(Term)根据自己在文档中的权重来影响文档相关性的打分计算。

于是我们把所有此文档中词(term)的权重(term weight) 看作一个向量。

Document = {term1, term2, …… ,term N}

Document Vector = {weight1, weight2, …… ,weight N}

同样我们把查询语句看作一个简单的文档，也用向量来表示。

Query = {term1, term 2, …… , term N}

Query Vector = {weight1, weight2, …… , weight N}

我们把所有搜索出的文档向量及查询向量放到一个N维空间中，每个词(term)是一维。

我们认为两个向量之间的夹角越小，相关性越大。

所以我们计算夹角的余弦值作为相关性的打分，夹角越小，余弦值越大，打分越高，相关性越大。

余弦公式如下：

 

下面我们假设：

查询向量为Vq = <w(t1, q), w(t2, q), ……, w(tn, q)>

文档向量为Vd = <w(t1, d), w(t2, d), ……, w(tn, d)>

向量空间维数为n，是查询语句和文档的并集的长度，当某个Term不在查询语句中出现的时候，w(t, q)为零，当某个Term不在文档中出现的时候，w(t, d)为零。

w代表weight，计算公式一般为tf*idf。

我们首先计算余弦公式的分子部分，也即两个向量的点积：

Vq*Vd = w(t1, q)*w(t1, d) + w(t2, q)*w(t2, d) + …… + w(tn ,q)*w(tn, d)

把w的公式代入，则为

Vq*Vd = tf(t1, q)*idf(t1, q)*tf(t1, d)*idf(t1, d) + tf(t2, q)*idf(t2, q)*tf(t2, d)*idf(t2, d) + …… + tf(tn ,q)*idf(tn, q)*tf(tn, d)*idf(tn, d)

在这里有三点需要指出：

• 由于是点积，则此处的t1, t2, ……, tn只有查询语句和文档的并集有非零值，只在查询语句出现的或只在文档中出现的Term的项的值为零。
• 在查询的时候，很少有人会在查询语句中输入同样的词，因而可以假设tf(t, q)都为1
• idf是指Term在多少篇文档中出现过，其中也包括查询语句这篇小文档，因而idf(t, q)和idf(t, d)其实是一样的，是索引中的文档总数加一，当索引中的文档总数足够大的时候，查询语句这篇小文档可以忽略，因而可以假设idf(t, q) = idf(t, d) = idf(t)

基于上述三点，点积公式为：

Vq*Vd = tf(t1, d) * idf(t1) * idf(t1) + tf(t2, d) * idf(t2) * idf(t2) + …… + tf(tn, d) * idf(tn) * idf(tn)

所以余弦公式变为：

下面要推导的就是查询语句的长度了。

由上面的讨论，查询语句中tf都为1，idf都忽略查询语句这篇小文档，得到如下公式

所以余弦公式变为：

下面推导的就是文档的长度了，本来文档长度的公式应该如下：

这里需要讨论的是，为什么在打分过程中，需要除以文档的长度呢？

因为在索引中，不同的文档长度不一样，很显然，对于任意一个term，在长的文档中的tf要大的多，因而分数也越高，这样对小的文档不公平，举一个极端的例子，在一篇1000万个词的鸿篇巨著中，"lucene"这个词出现了11次，而在一篇12个词的短小文档中，"lucene"这个词出现了10次，如果不考虑长度在内，当然鸿篇巨著应该分数更高，然而显然这篇小文档才是真正关注"lucene"的。

然而如果按照标准的余弦计算公式，完全消除文档长度的影响，则又对长文档不公平(毕竟它是包含了更多的信息)，偏向于首先返回短小的文档的，这样在实际应用中使得搜索结果很难看。

所以在Lucene中，Similarity的lengthNorm接口是开放出来，用户可以根据自己应用的需要，改写lengthNorm的计算公式。比如我想做一个经济学论文的搜索系统，经过一定时间的调研，发现大多数的经济学论文的长度在8000到10000词，因而lengthNorm的公式应该是一个倒抛物线型的，8000到 10000词的论文分数最高，更短或更长的分数都应该偏低，方能够返回给用户最好的数据。

在默认状况下，Lucene采用DefaultSimilarity，认为在计算文档的向量长度的时候，每个Term的权重就不再考虑在内了，而是全部为一。

而从Term的定义我们可以知道，Term是包含域信息的，也即title:hello和content:hello是不同的Term，也即一个Term只可能在文档中的一个域中出现。

所以文档长度的公式为：

代入余弦公式：

再加上各种boost和coord，则可得出Lucene的打分计算公式。

6. 总结

    前面学习了Solr的评分机制，虽然对理论的推导以及公式有了一些了解，但是在Solr具体实现上我却产生了不少疑惑：

    1. BooleanQuery查询，为什么没有用到LengthNorm。

    2. BooleanQuery 多条件查询时候，Not And Or 对文档进行打分时候是否具有影响。

    3. PharseQuery查询时候，打分又是怎么进行的。

    4. 怎么样对这个进行打分进行定制。

    这些都是接下来需要去理解的。