洛谷P1282 多米诺骨牌
题目描述
多米诺骨牌有上下2个方块组成,每个方块中有1~6个点。现有排成行的
上方块中点数之和记为S1,下方块中点数之和记为S2,它们的差为|S1-S2|。例如在图8-1中,S1=6+1+1+1=9,S2=1+5+3+2=11,|S1-S2|=2。每个多米诺骨牌可以旋转180°,使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。
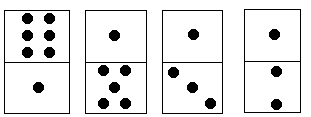
对于图中的例子,只要将最后一个多米诺骨牌旋转180°,可使上下2行点数之差为0。
输入输出格式
输入格式:
输入文件的第一行是一个正整数n(1≤n≤1000),表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数,表示多米诺骨牌上下方块中的点数a和b,且1≤a,b≤6。
输出格式:
输出文件仅一行,包含一个整数。表示求得的最小旋转次数。
输入输出样例
输入样例#1:
4
6 1
1 5
1 3
1 2
输出样例#1:
1
Solution
先打了个搜索?45分
#include<bits/stdc++.h>
using namespace std;
const int N=1010,inf=2e9;
int n,tot,ans=inf,tq=inf;
int a[N],b[N];
void dfs(int x,int sum,int cnt) {
if(x==n+1) {
if(abs(tot-sum-sum)<ans) ans=abs(tot-sum-sum),tq=cnt;
else if(abs(tot-sum-sum)==ans) tq=min(tq,cnt);
return;
}
dfs(x+1,sum+a[x],cnt);
dfs(x+1,sum+b[x],cnt+1);
}
int main()
{
ios::sync_with_stdio(0);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i]>>b[i],tot+=a[i]+b[i];
dfs(1,0,0);
cout<<tq<<endl;
}
为什么要贴这份代码,因为我们可以把我们搜索中记录的变量变成dp中的状态(一位dalao告诉我的做dp的方法?)
我们发现因为当题目给出塔牌的点数后,无论是否翻转,前i张牌的上下点数之和是不变的,那么我们知道一个就可以求出另一个
ok?我们现在来设计(dp)数组,按照搜索中的变量,设dp[i][j]表示到第i张纸牌,第一行的和为j的翻转次数
那么状态转移方程就呼之欲出了?
(dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]])) 这是不翻转的情况
(dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1)) 翻转
我们发现这样转移可能会越界?那就加个条件嘛
if(j-a[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]]);
if(j-b[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1);
那么初始化,第二维最大可能是6*n(每张都是6点),所以初始化
for(int i=1;i<=n;i++)
for(int j=0;j<=6*n;j++) dp[i][j]=inf;
然后就是dp边界
dp[1][b[1]]=1,dp[1][a[1]]=0;//为什么是这个顺序,因为如果先a后b,那么当第一张纸牌上下点数相同时,dp[1][a[1]]会被赋值成1
最后枚举一下点数统计答案就可以了,和dfs一样
Code
#include<bits/stdc++.h>
using namespace std;
const int N=1010,inf=2e5;
int n,tot,ans=inf,tq=inf;
int a[N],b[N],dp[N][6*N];
int main()
{
ios::sync_with_stdio(0);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i]>>b[i],tot+=a[i]+b[i];
for(int i=1;i<=n;i++)
for(int j=0;j<=6*n;j++) dp[i][j]=inf;
dp[1][b[1]]=1,dp[1][a[1]]=0;
for(int i=2;i<=n;i++) {
for(int j=0;j<=6*n;j++) {
if(j-a[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]]);
if(j-b[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1);
}
}
for(int i=0;i<=tot;i++) {
if(dp[n][i]!=inf) {
if(abs(tot-i-i)<ans)
ans=abs(tot-i-i),tq=dp[n][i];
else if(abs(tot-i-i)==ans) tq=min(tq,dp[n][i]);
}
}cout<<tq<<endl;
}