(1)激活函数
激活函数(Activation function)并不是指这个函数去激活什么,而是指如何把“激活的神经元的特征”通过函数把特征保留映射出来。对输入信息进行非线性变换。
线性模型的最大特点是任意线性模型的组合仍然还是线性模型。只通过线性模型,任意层的全连接神经网络和单层神经网络模型的表达能力没有任何区别。线性模型最大的局限性是表达能力不够,解决的问题有限。线性模型就能解决线性可分问题。
常用激活函数
1)sigmoid函数(曲线很像“S”型)
公式:
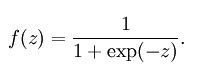
曲线图:
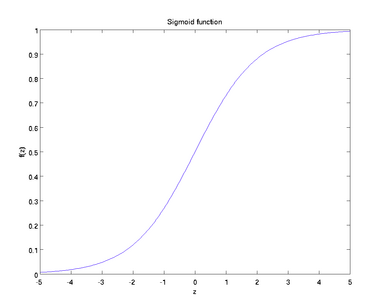
sigmoid函数也叫Logistic函数,将一个实数映射到(0,1)的区间,可以用做二分类。
sigmoid函数对中央区的信号增益较大,对两侧区的信号增益小,在特征相差比较复杂或是相差不是特别大时效果比较好。
sigmoid函数缺点:
激活函数计算量大,反向传播求误差梯度时,求导涉及除法
反向传播时,很容易就会出现梯度消失的情况,从而无法完成深度网络的训练。(sigmoid的饱和性)
为什么出现梯度消失:
反向传播算法中,要对激活函数求导,sigmoid的导数表达式为:
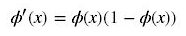
sigmoid原函数及导数图形如下:
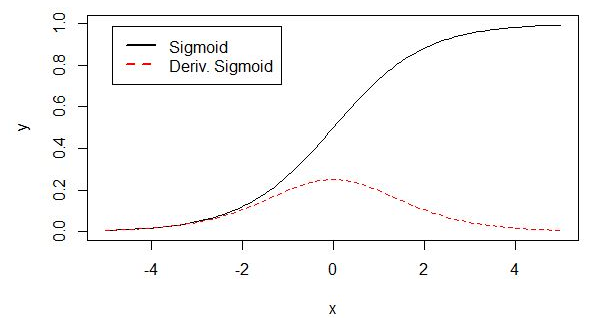
从上图可以看到,其两侧导数逐渐趋近于0,具有这种性质的称为软饱和激活函数。
一旦输入落入饱和区,sigmoid函数的导数就会变得接近于0,导致向底层传递的梯度也变得非常小,网络参数很难得到有效锻炼。这种现象称为梯度消失。sigmoid激活函数在网络5层之内就会产生梯度消失现象。 一般,sigmoid函数在网络5层之内就会产生梯度消失现象。
sigmoid函数的输出均大于0,使得输出不是0均值,称为偏移现象,这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。
2)Tanh函数
公式:
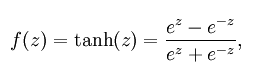
曲线图:
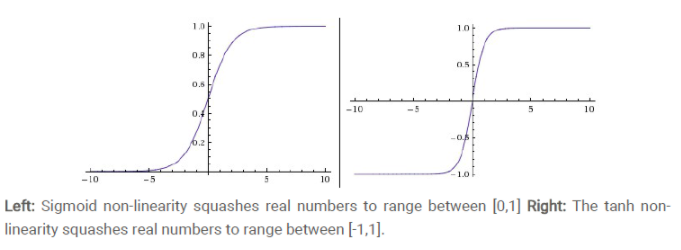
Tanh函数又称双曲正切函数,取值范围为[-1,1]
Tanh函数在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。
与sigmoid函数的区别是,tanh函数是0均值的,因此实际应用中tanh会比sigmoid函数更好,然而,tanh函数一样具有软饱和性,造成梯度消失。
3)ReLU函数
公式:
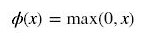
曲线图:
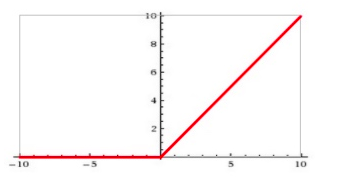
当输入信号小于等于0时,输出都是0;当输入信号大于0时,输出等于输入。
ReLU函数优点:
使用ReLU得到的SGD(随机梯度下降)的收敛速度会比sigmoid/tanh快很多。此外,当x<0时,ReLU函数硬饱和;当x>0时,则不存在饱和问题。所以,ReLU函数能够在x>0时保持梯度不衰减,从而缓解梯度消失问题。
ReLU函数缺点:
随着训练的推进,部分输入会落入硬饱和区,导致对应权重无法更新。这种现象被称为“神经元死亡”。与sigmoid类似,ReLU的输出均值也大于0,偏移现象和神经元死亡会共同影响网络的收敛性。
4)softmax函数
公式:

模型图:
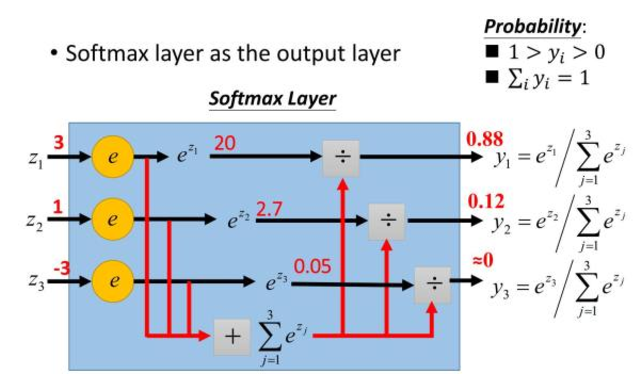
主要用于多分类,它将多个神经元的输出,映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类!