1.Problem and Loss Function
Linear Regression is a Supervised Learning Algorithm with input matrix X and output label Y. We train a system to make hypothesis, which we hope to be as close to Y as possible. The system we build for Linear Regression is :
hθ(X)=θTX
From the initial state, we probably have a really poor system (may be only output zero). By using X and Y to train, we try to derive a better parameter θ. The training process (learning process) may be time-consuming, because the algorithm updates parameters only a little on every training step.
2. Cost Function?
Suppose driving from somewhere to Toronto: it is easy to know the coordinates of Toronto, but it is more important to know where we are now! Cost function is the tool giving us how different between Hypothesis and label Y, so that we can drive to the target. For regression problem, we use MSE as the cost function.
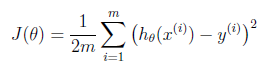
This can be understood from another perspective. Suppose the difference between Y and H is ε, and ε~N(0,σ2). So, y~N(θTX,σ2). Then we do Maximum Likelihood Estimate, we can also get the same cost function. (https://stats.stackexchange.com/questions/253345/relationship-between-mle-and-least-squares-in-case-of-linear-regression)
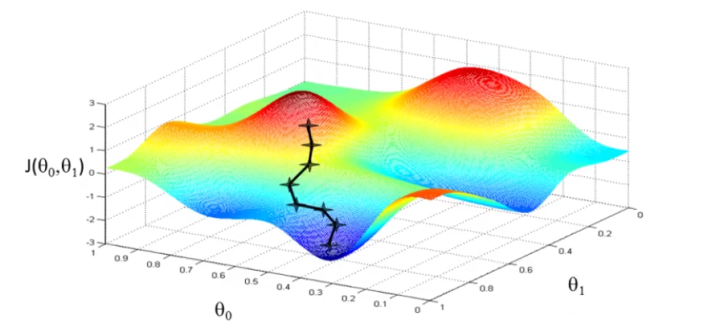
3.Gradient Descent
The process of GD is quite like go downhill along the steepest direction on every dimension.
We take derivatives along every dimension
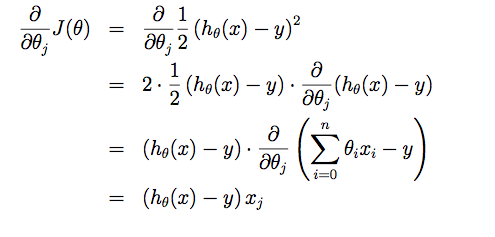
Then update all θ by a small learning rate alpha simultaneously:

4. Batch Learning, Stochastic and Mini Batch
In above, we use all the training examples together to calculate cost function and gradient. This method is called 'Batch Gradient Descent'. The issue here is: what if there is a exetremely large data set? The training process can be quitely long. A variant is called Stochastic Gradient Descent, also 'Online Learning'. Every time when it trains, the algorithm only uses a single training example, which may result in very zigzagged learning curve. Finally, the most popurlar version:' Mini-Batch Gradient Descent'. It chooses a small group of training example to learn, so the speed is OK, and the learning curve is more smooth.