其实几何类的问题也可以分成两大类,不仅仅所有的几何问题都是叉积和设计繁琐的穷举,也会出现一些很偏几何的题目,这种时候,进行充分的数理分析是非常重要的。
Q1:
修水管问题:
话说最近柴小俊迷上了一款战略经营游戏《部落冲突》,他在修建筑的时候面临这样一个问题,他的军营被夹在两条河流之间,现在它想在两条河流的边上修筑供水点,并且需要用水管将两个供水点分别与军营连接起来(两个供水点之间也要相连),那么身为Acmer的你,能否当一次参谋,告诉柴小俊他最少需要准备多长的水管呢?
输入:我们以一条河流为x轴建系数,两条河流在(0,0)交汇。
点A的坐标(另一条河流上的一点,假定其在第一象限)。
点B的坐标(数据保证它落在两条直线的内部)。
输出:
输出柴小俊修建水管的最小长度。
分析:我们首先要做的应该是将这个实际问题抽象成数学(几何)问题,很容易看到,这道问题描述的是如下一个图形。
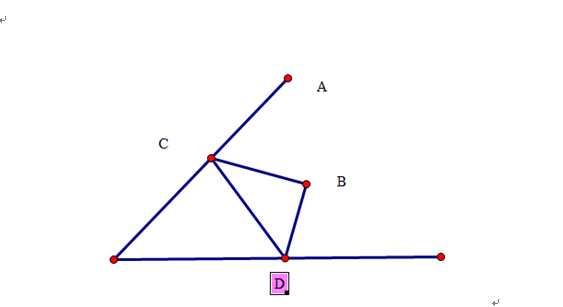
给出了直线OA,和夹在x、OA之间的B,那么现在需要你求解三角形BCD的最小周长,其中C、D必须分别落在OA和x轴上。
首先我们先进行最优解的分析,也就是我们得找到这个最优三角形。我们任意画一个三角形BCD,很容易看到,这里我们分别做B关于OA、x轴的对称点,记作E、F,那么根据中垂线的性质,我们发现三角形的周长变成了DC+CD+DF,那么为了使得和最小,应该令E、C、D、F共线,也就是说,连接E、F,与OA、x的交点就是最优三角形的顶点C、D。
那么现在问题的关键变成了怎么求一个点关于一条直线的对称点(点A关于直线l的对称点B)。
容易看到,我们可以把这个过程分为两个过程:
(1) 作点关于A在直线l上的投影,记作C。
(2) 基于投影,我们进行向量运算,点C + 向量CA。(想一想,为什么)
那么我们的问题再次简化:如何求A在l上的投影?
这里就需要进行一些简单的运算。

有了这些铺垫,我们就不难求得两个对称点,它们之间的距离也就是这道问题的最终解。
Q2:
等周问题.
话说柴小俊成功修完水管之后,实力大增(节省了材料),成功攻占了地方阵营,经过谈判,在敌方阵营中(一个三角形区域),柴小俊能够用长度为L的绳子圈出一块区域作为自己的领地,那么机智的你,能否告诉柴小俊他最多能够圈多大的面积呢?
输入:
给出三角形三个顶点的坐标、 绳长L。
输出:
柴小俊能够圈出的最大面积。
分析:首先我们脱离这个具体问题本身,来想清楚另外一个问题:周长L的所有平面几何图形中,面积最大的是谁?
其实这就是著名的等周问题,答案是圆。其最严谨的证明在数学分析的课本中往往会介绍变分法来证明,但是这里我们利用一个初等的技巧来简单的证明一下。
证明:
首先我们能够看到,最大面积的图形必然是“凸型曲线”,因为如果是凹陷的,我们能够将凹陷处向外翻折,周长没变但是显然面积增大了。
其次,我们应该看到,最大面积图形中,任取一点A,再做另外一点B,使得曲线AB的长度是L的一半,直线AB左右两侧的面积应该是相同的。因为如果不同,我们可以做那个面积较大的部分关于AB的对称,依然是周长没变,面积变大。
最后,基于上边的要点,我们发现,只要找到了不闭合曲线L/2和直线AB围成图形的最大面积,那么我们通过对称就可以得到最终的最大面积图形。这里在长度为L/2的不闭合曲线上取一个点C,假设这里弦AC及其对应的弧围成的面积是最大的、BC及其对应的弧围成的面积是最大的,那么现在最优解的问题又转化了:一直三角形的两边AC、BC,△ABC的最大面积是多少?很显然,由三角形的面积公式S=1/2absinC可知,C是直角的时候面积最大。那么在这段弧上处处取这样的点,都要满足这个结论,最终我们会得到一个半圆。
最后我们就得到了一个圆。
证毕。
那么我们现在再次回到这个问题,会出现如下三种情况:
(1)L小于三角形内切圆的周长,那么这表明L可以在三角形内部圈出一个完整的圆。
(2)L大于三角形的周长,那么圈出的面积就是这个三角形。
(3)介于二者之间。
能够看到,对于(1)(2)两种情况非常好处理,难处理的是(3)。
看这样一个图。
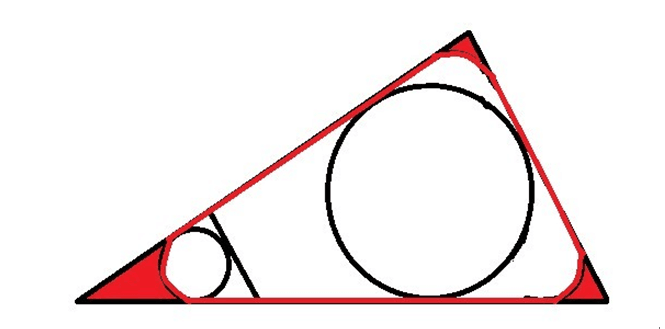
首先我们要搞明白这种情况下的曲线的性质。
这里首先确定这样一件事情:图中直线部分的长度和曲线部分长度分别都是定值,然后对于曲线部分,利用等周定理,我们应该拼出一个圆才能够使得面积最大。
也就是我们得到这样要给结论,这种情况下最大面积的图形,三段曲线是一个整圆的三部分。
然后依据性质做具体而有效的计算。
S(白) = S(大三角)-S(小三角)+S(小内切圆)
结合初等数学相似比的方法,便可求解。
简单的参考代码如下:
#include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; const double eps=1e-9; const double pi=acos(-1.0); double a, b, c, l; bool cmp(double a , double b) { return a < b ? 1 : 0; } int main() { double len, hl, cosc, area, res, r, k; int tt=1; double edge[3]; while(scanf("%lf%lf%lf%lf", &edge[0], &edge[1], &edge[2], &l) != EOF) { if(fabs(edge[0])<eps && fabs(edge[1])<eps && fabs(edge[2])<eps && fabs(l)<eps) break; sort(edge,edge + 3,cmp); a = edge[0],b = edge[1] , c = edge[2]; len=a+b+c; cosc=(a*a + b*b - c*c)/(2*a*b); if(fabs(cosc)<eps) area=a*b/2 , r=(a+b-c)*0.5; else area=a*b*sqrt(1-cosc*cosc)*0.5, r=area*2.0/len; if(2*pi*r>=l) { r = l/(2*pi); res = pi*r*r; } else if(l>=len) res=area; else { k=(len-l)/(len-2*pi*r); r*=k; res=area-area*k*k+pi*r*r; } printf("Case %d: %.2lf ", tt++, res); } return 0; }