之前关于二重积分的笔记,介绍了二重积分概念的引入,但是对于它的计算方法(化为累次积分),介绍的较为模糊,它在《概率论基础教程》中一系列的推导中发挥着很重要的作用。
回想先前关于二重积分的几何含义,求解一个曲顶圆柱的体积,我们用如下的符号进行定义:
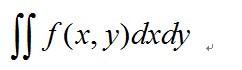
现在我们通过另外一条路径,再次得到几何体的体积,便可以建立等式,那么对于一般的二重积分,我们就找到了计算方法。
看这样一个图:
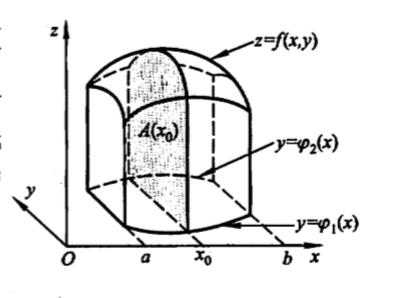
落在x-O-y上的面积就是被积区域D,几何体的顶部z=f(x,y)就是被积函数,为了求解这个几何体的体积,我们采取先求侧面面积(平行于y-O-z面),然后对基于所求结果再对x进行积分,便得到了几何体的体积。
侧面积A(x0):
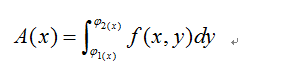
简单的一维积分求解曲边梯形。
随后基于这个侧面积的结果再对x积分,显然就得到了体积,等式如下。
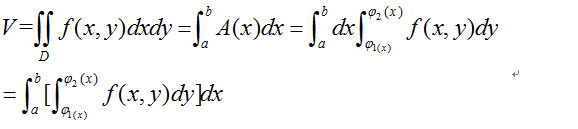
那么我们就将重积分化为了累次积分,在上述形式中,最后两个等号后边的形式都表示先对y积分然后对x积分。
需要注意,按照这种极限法表示几何的体积,对它的底面是有限制的,它分为X型积分区域和Y型积分区域,例如在上面的图中,是一个X型积分区域。
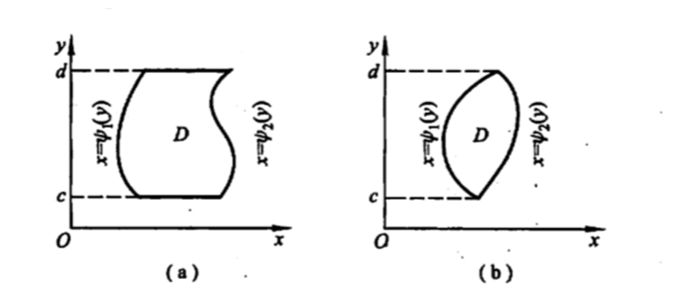
Y型积分区域:
X型积分区域:
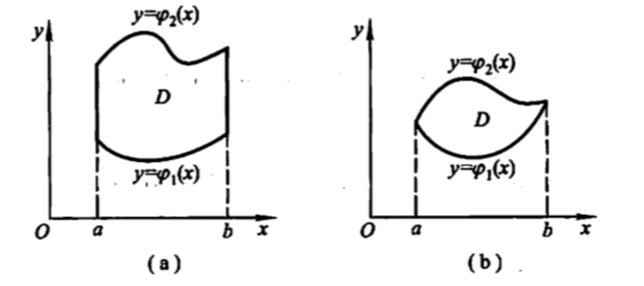
那么很显然,如果对于某个积分区域既满足X型又满足Y型,那么我们有如下的等式成立:

这个定理其实就是傅比尼定理增强形式,它是二重积分算法的基础,同时也是等价交换积分次序的基础。

这两种情况其实就是呼应着上面的X型和Y型积分区域,当某种情况既是X型积分区域又是Y型积分区域,那么便可以根据积分计算的便捷性进行积分次序的交换,而如果既不是X型也不是Y型,则考虑通过分割法将被积区域R变为X型与Y型的加和。其正确性结合上文关于二重积分几何意义的算法过程,是不言自明的。