Horn–Schunck光流算法[1]是一种全局方法估算光流场。
参考博文:https://blog.csdn.net/hhyh612/article/details/79216021
假设条件:
HS算法除了需要满足LK光流前两个假设之外,增加了一个假设条件:
场景中属于同一物体的像素形成光流场向量应当十分平滑,只有在物体边界的地方才会出现光流的突变,但这只占图像的一小部分,总体上来看图像的光流场应当是平滑的。
数学原理推导:
仍然是两帧图像I(x, y, t), 和I(x+δx, y+δy, z+δz, t+δt )。要求他们之间的光流场V(u, v):
首先定义一个能量函数, 如下:
![]()
这个能量函数的前半部分是灰度变化因子,如下:
![]()
后半部分是平滑因子,如下:
![]()
理想的光流场,应该使这两项的值最小:即灰度变化小(亮度恒定)并且速度变化小(小运动)。
这是一个泛函的极值问题,可以用欧拉-拉格朗日方程求解。对应上式的是双变量双函数一阶导数的欧拉-拉格朗日方程组
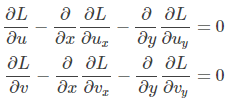
其中上式中:
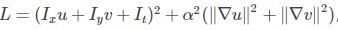
求导, 得到下式:
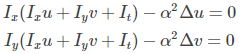
上式中Δ是拉普拉斯算子操作:
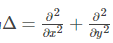
实际计算中可以用下面的式子代替拉普拉斯操作:
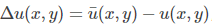
拉普拉斯操作替换后化简为下式:

这是一个线性方程组,但是首先要求取u,v的均值,然而u, v的均值也是未知的,因此可以继续化简上式,分别消去u和v,得到下面的迭代公式:
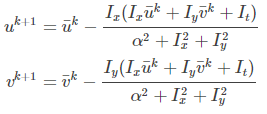
有了迭代公式后,u, v均值的初始值为0,计算出u, v值,然后依次迭代。直到满足如下条件,退出迭代,得到光流u, v值:
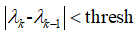
其中:
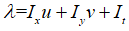
源码及效果:
源码链接:https://blog.csdn.net/xiaoyufei117122/article/details/53693627
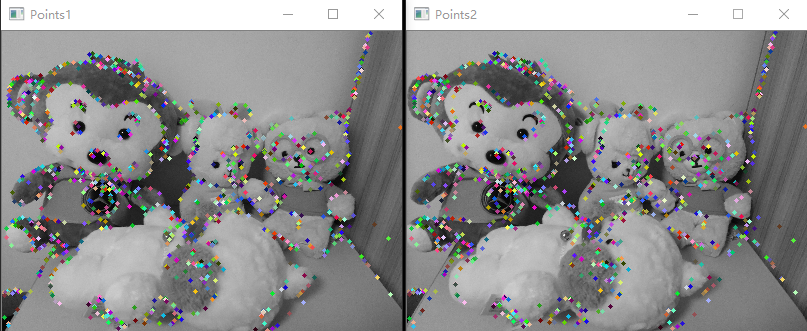
效果如下:
[1] B.K.P. Horn and B.G. Schunck, “Determining optical flow.” 1981